Data Frames - Part 1

Figure 1

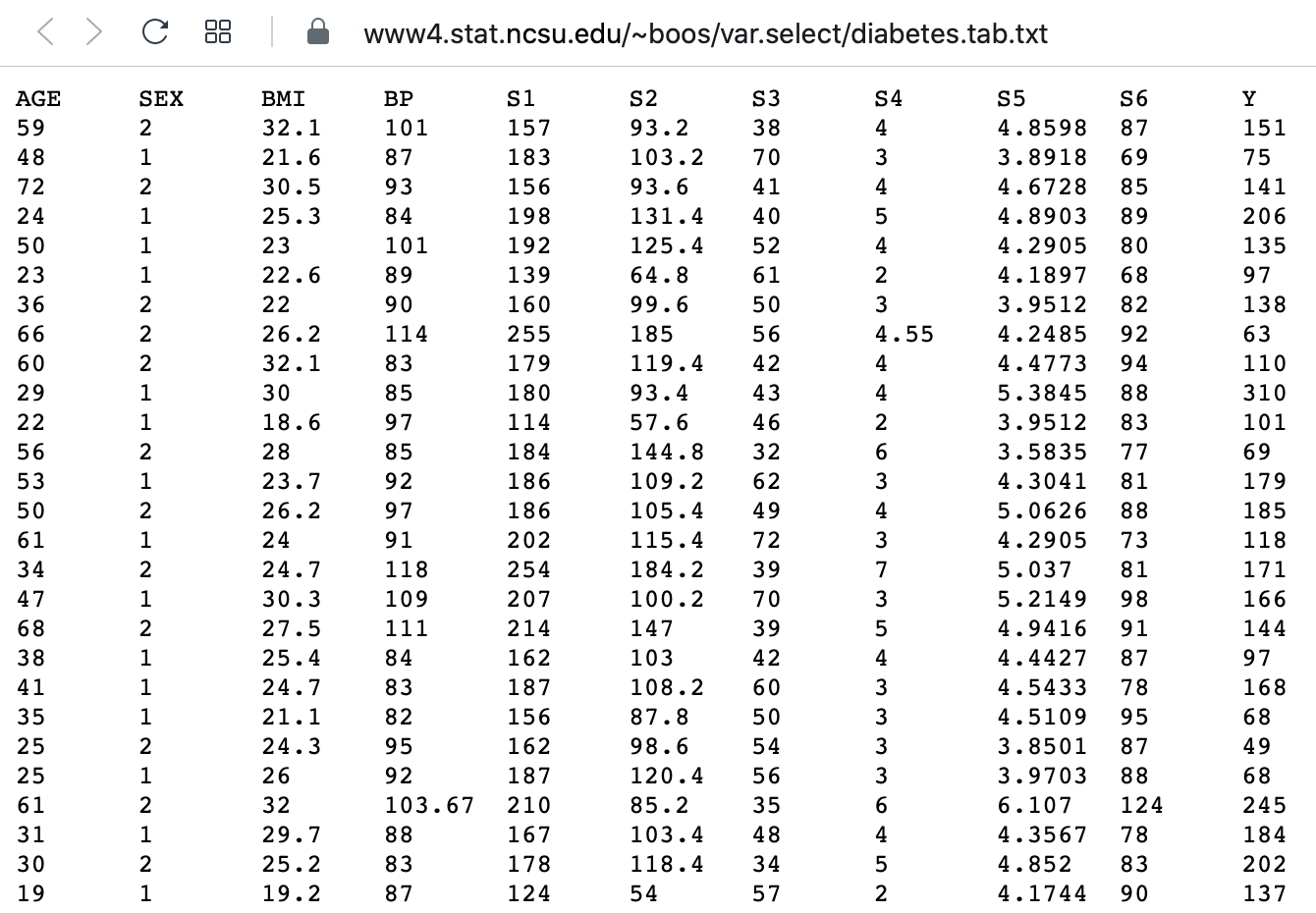
Figure 2

Figure 3

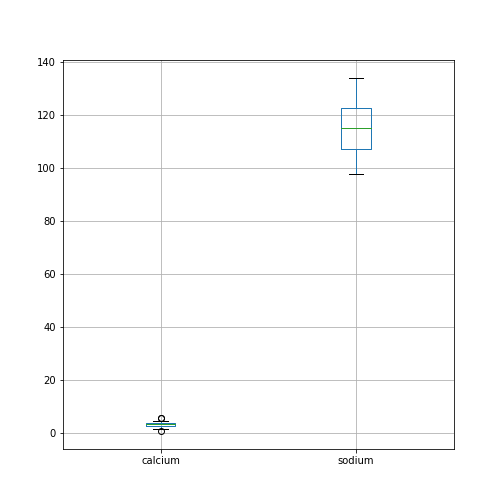
Figure 4

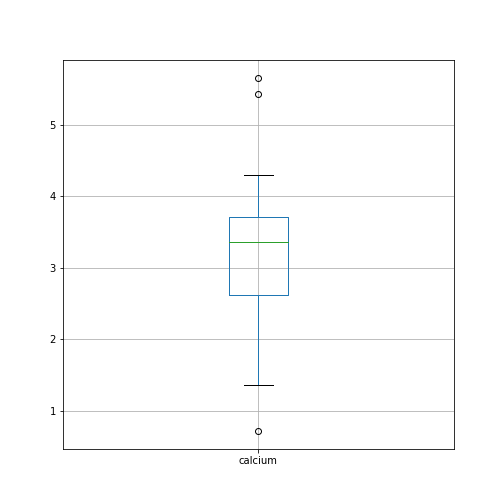
Figure 5

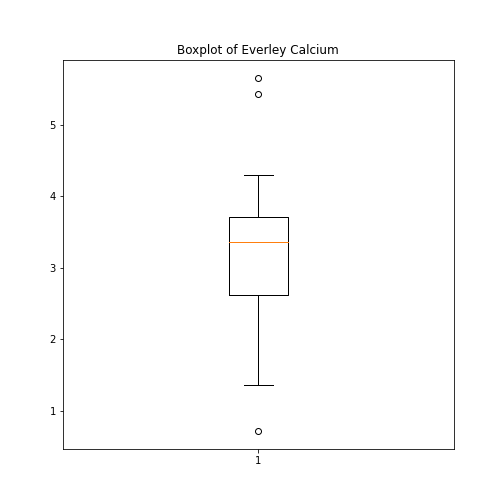
Figure 6

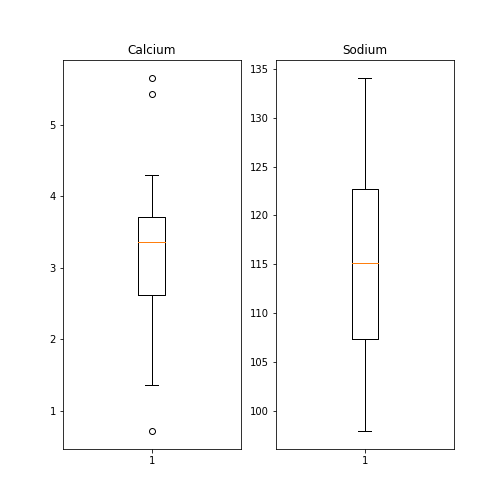
Figure 7

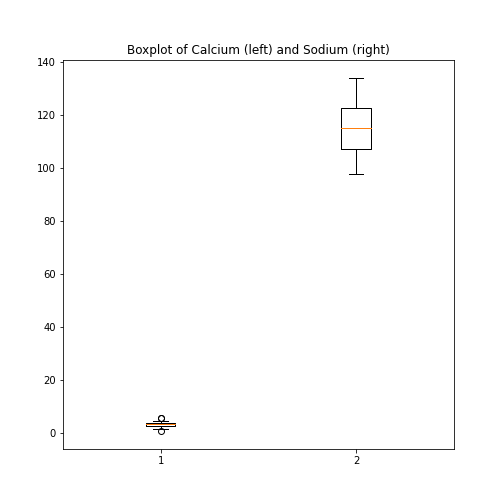
Figure 8

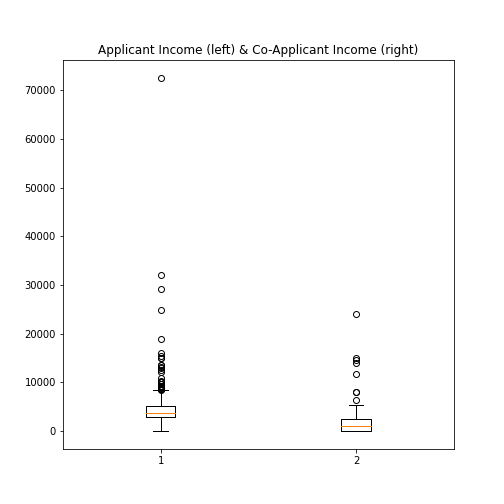
Figure 9

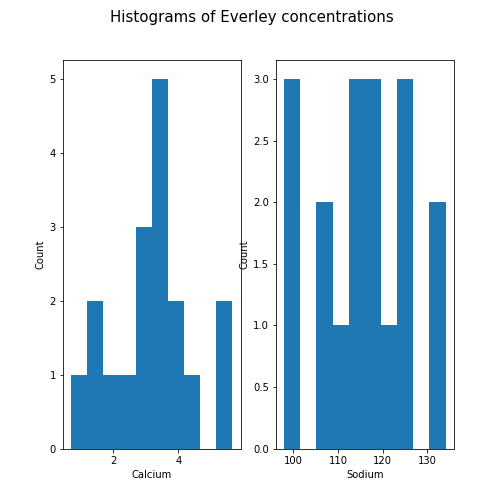
Figure 10

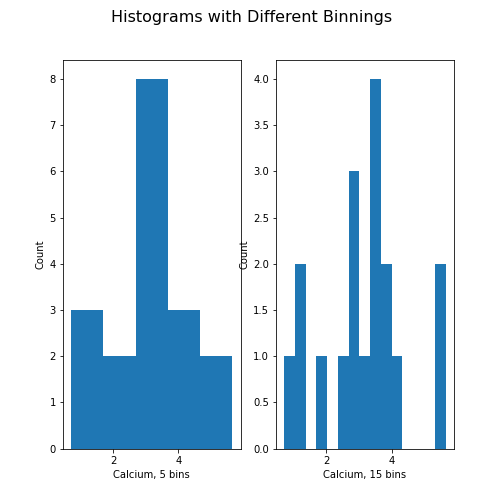
Figure 11

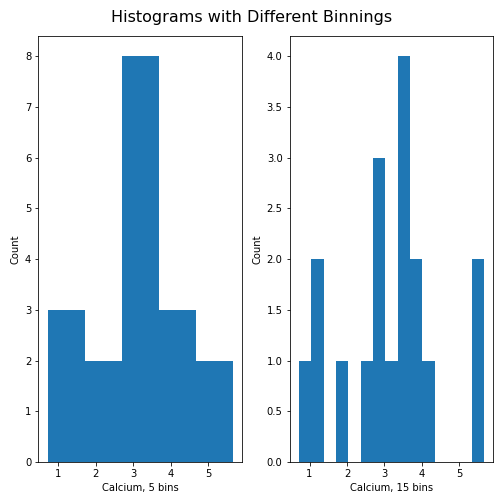
Figure 12

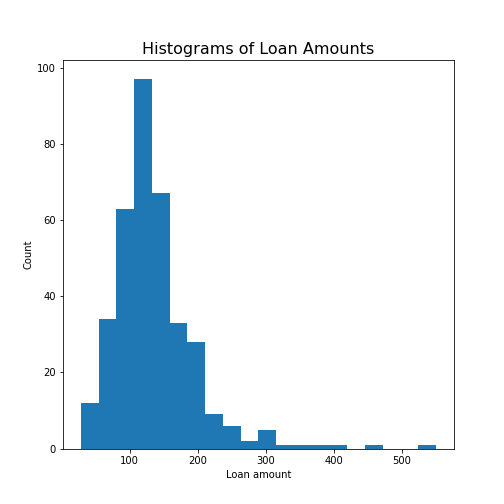
Figure 13

Figure 14

Data Frames - Part 2

Figure 1

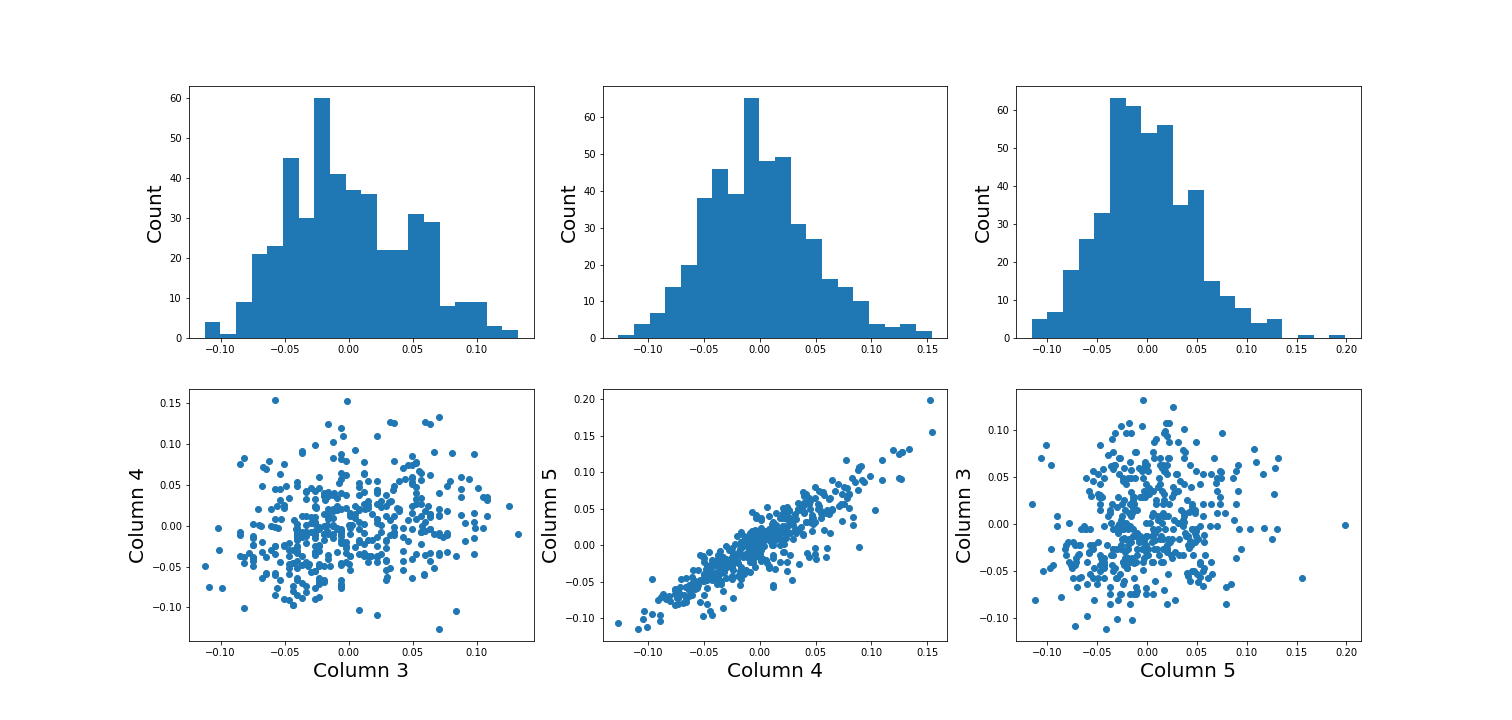
Figure 2

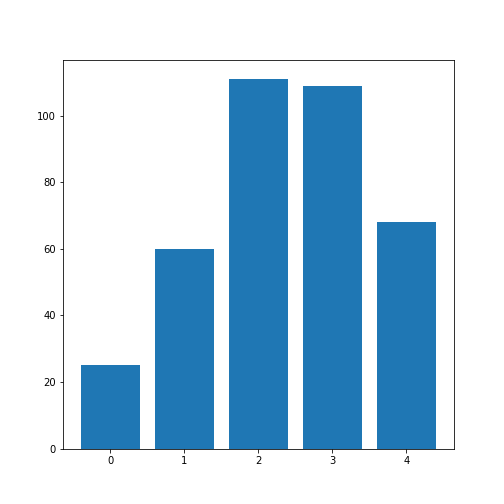
Figure 3

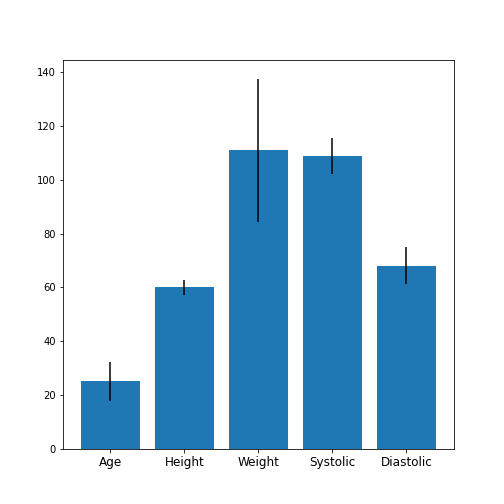
Figure 4

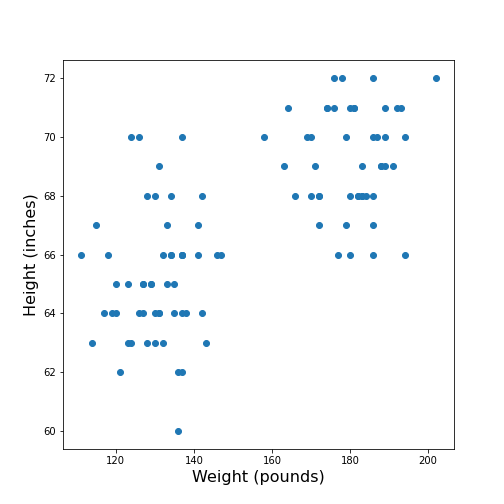
Figure 5

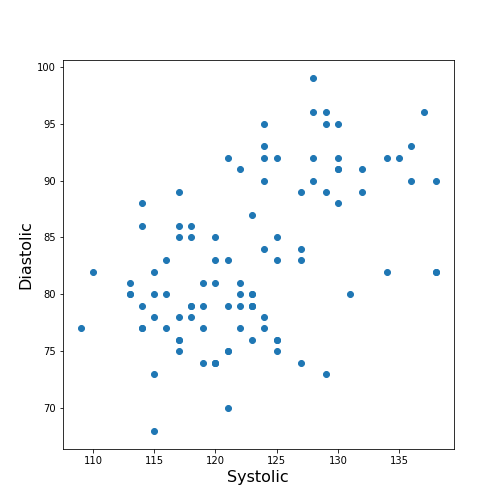
Figure 6

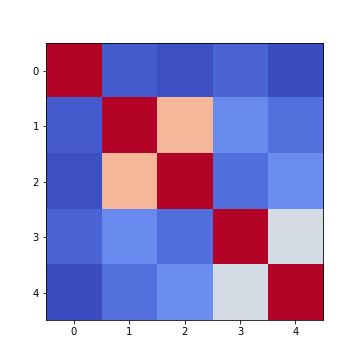
Figure 7

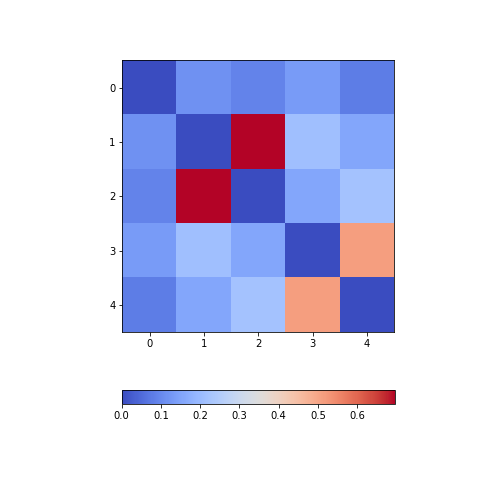
Figure 8

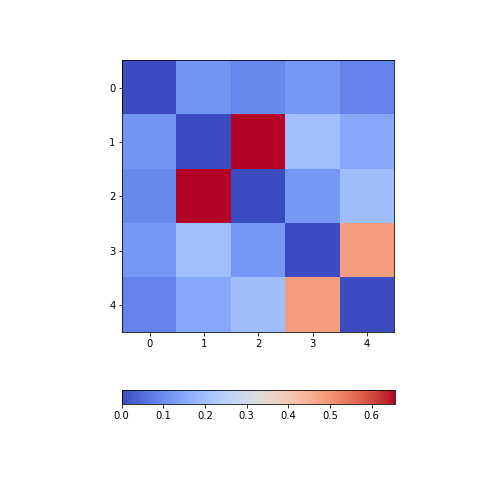
Figure 9

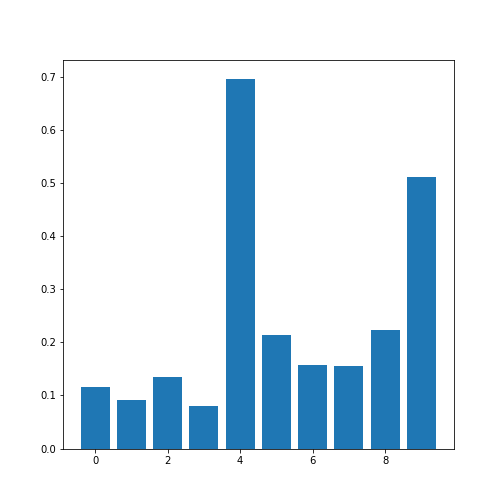
Figure 10

Figure 11

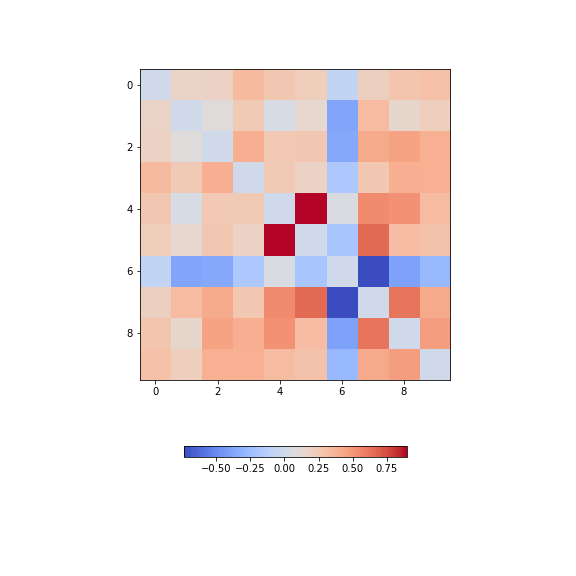
Figure 12

Figure 13

Figure 14

Figure 15

Figure 16

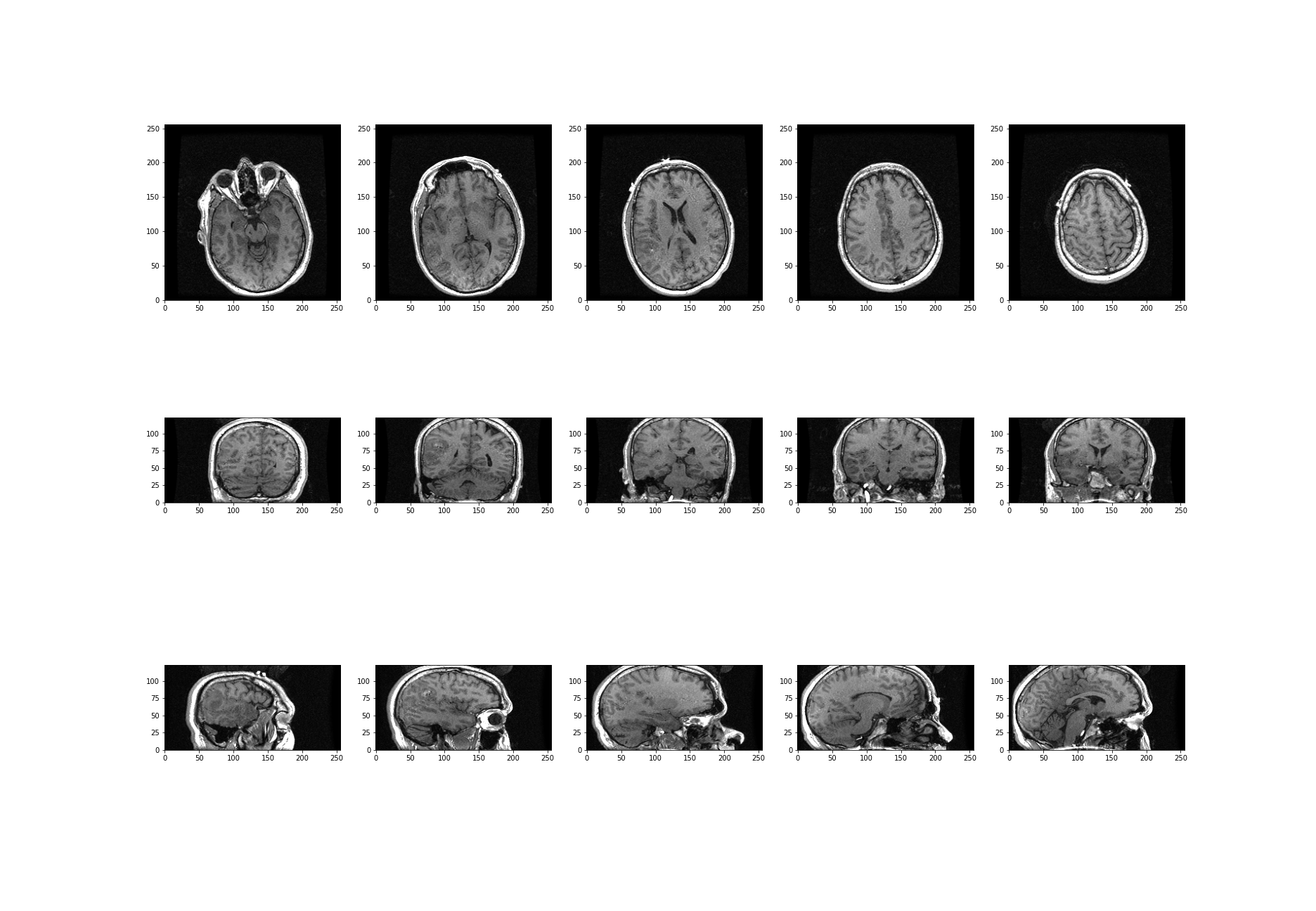
Image Handling

Figure 1

Figure 1: Example image, rat cerebellum
Figure 1: Example image, rat cerebellum

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

Figure 11

Figure 12

Figure 13

Figure 14

Figure 15

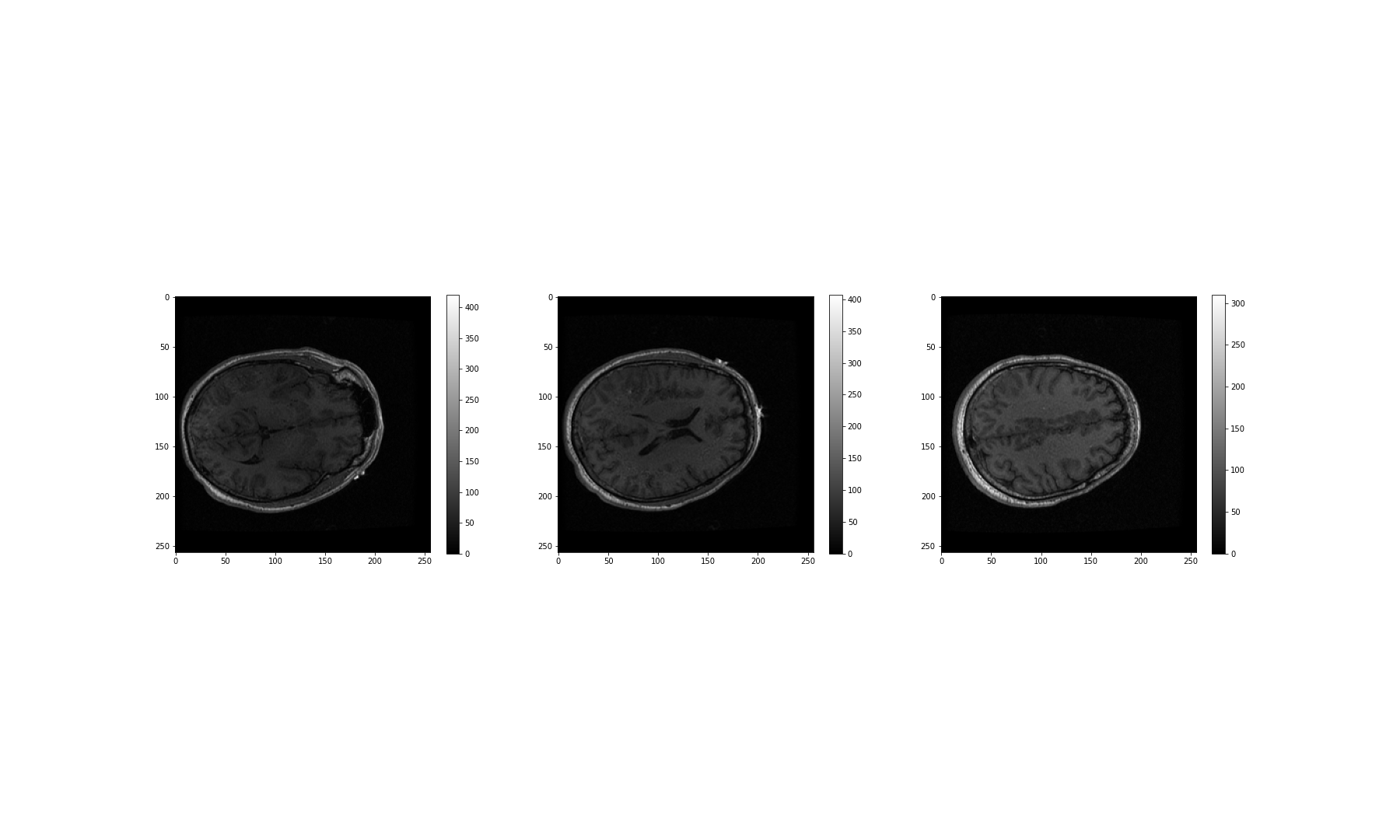
Figure 16

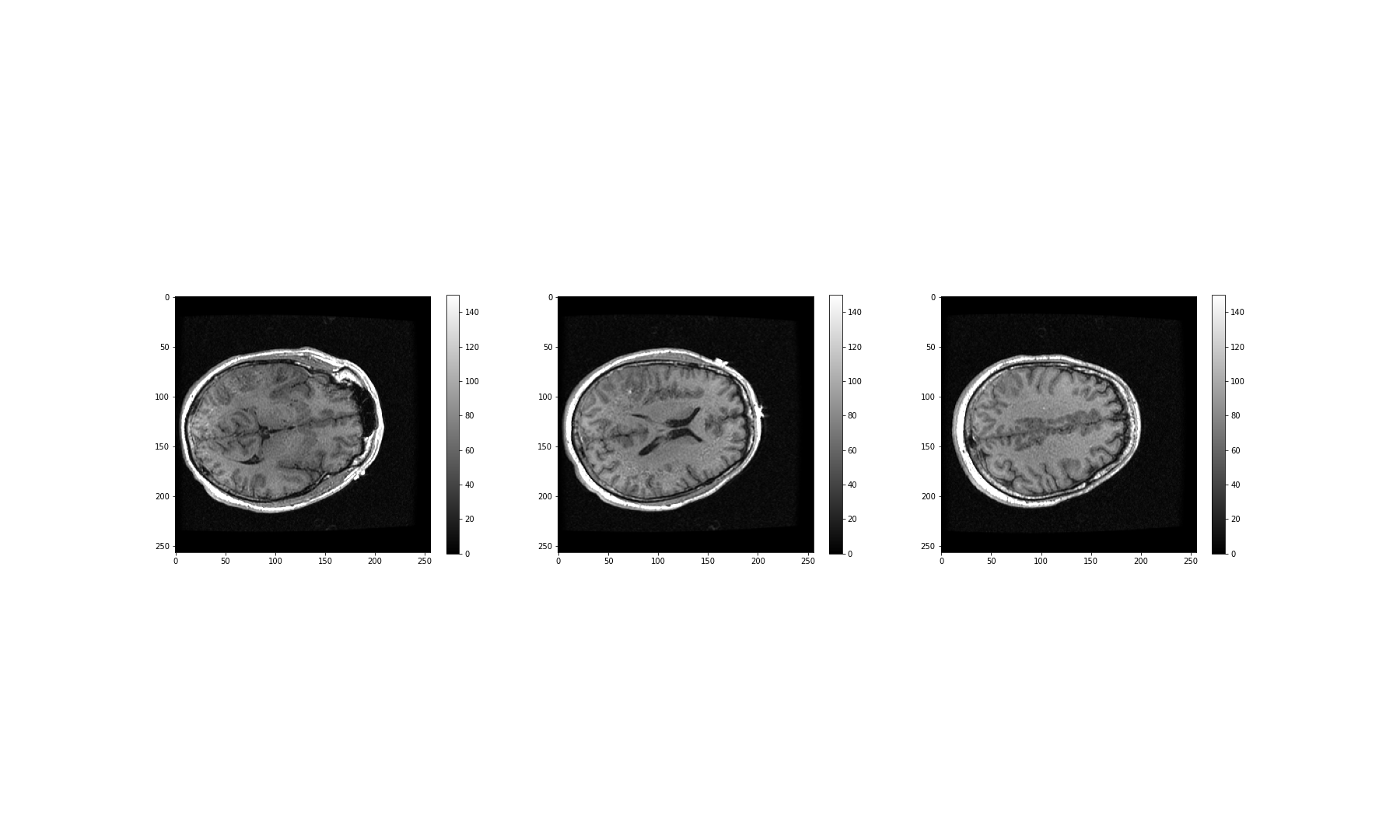
Figure 17

Figure 18

Figure 19

Figure 20

Figure 21

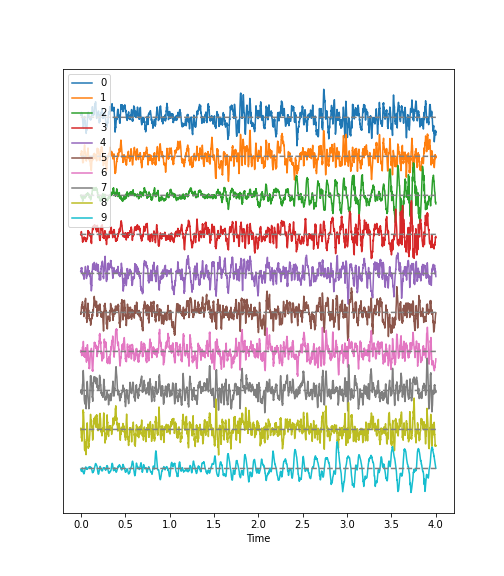
Time Series

Figure 1

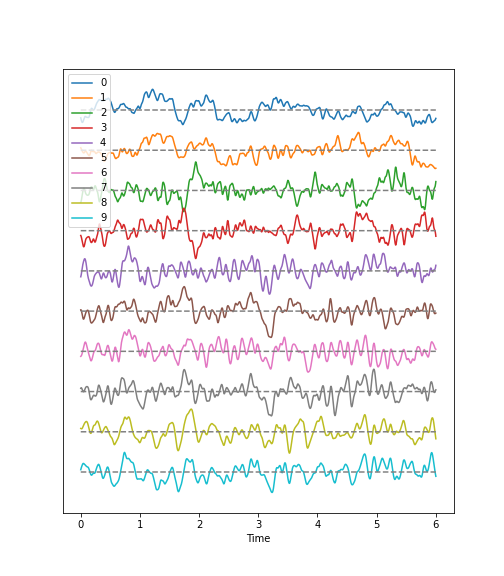
Figure 2

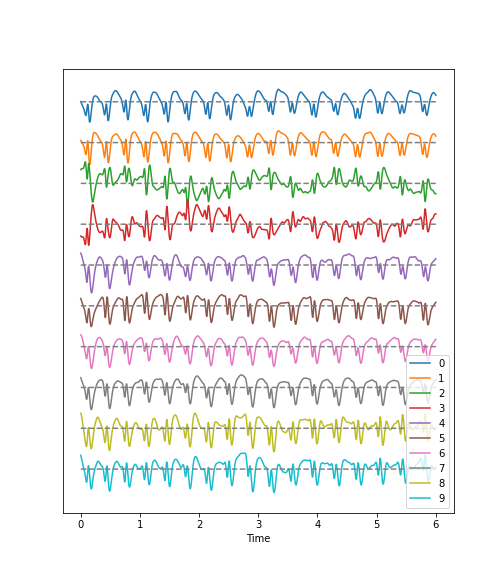
Figure 3

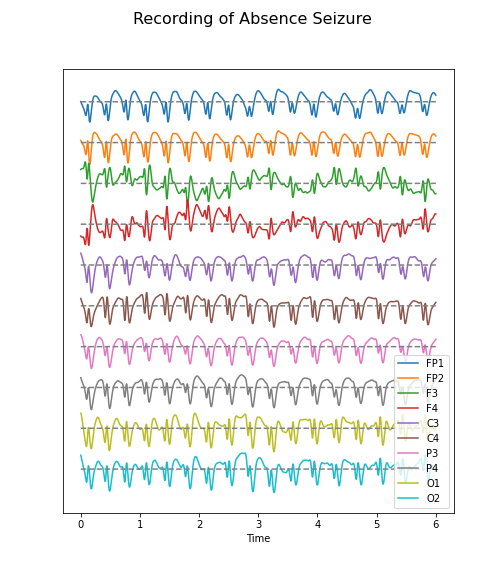
Figure 4

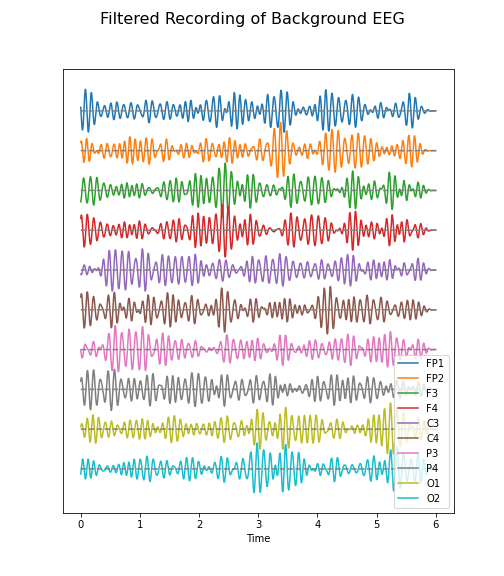
Figure 5

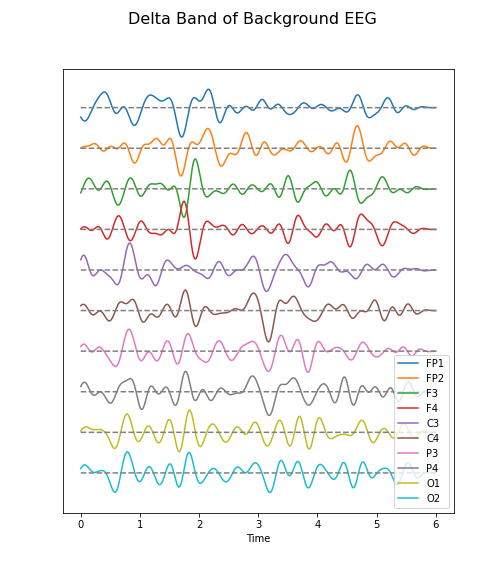
Figure 6

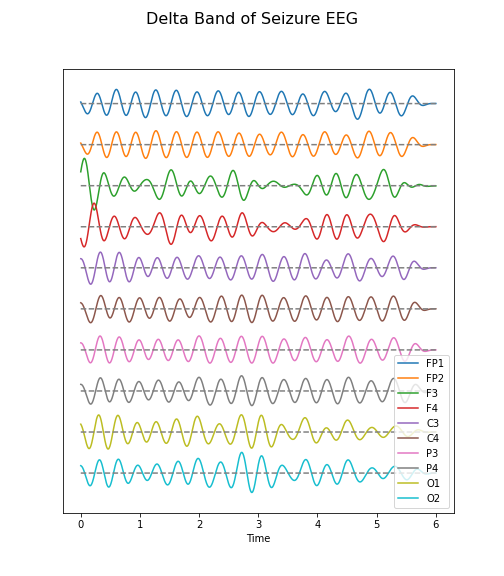
Figure 7

Fourier Transform of EEG data

We import the Fourier transform function fft from scipy.fftpack and can use it to transform all columns at the same time.

PYTHON 

from scipy.fftpack import fft

data_back_fft = fft(data_back, axis=0)
To plot the results, a couple of steps are required.

First, we obtain a Fourier spectrum for every data column, so we need to define how many plots we want to have. If we take only columns, we can display them all in one go.

Second, the Fourier transform results in twice the number of complex coefficients (positive and negative) of which we only need the first half.

Third, the Fourier transform outputs complex numbers. To display the ‘amplitude’ of a frequency (the coefficient corresponding to the amplitude of the sine wave with that frequency) we take the absolute value of the complex numbers.

PYTHON 

no_win = 2

rows = data_back.shape[0]

freqs = (sr/2)*linspace(0, 1, int(rows/2))

amplitudes_back = (2.0 / rows) * abs(data_back_fft[:rows//2, :2])


fig, axes = subplots(figsize=(6, 5), ncols=1, nrows=no_win, sharex=False)

names = df_back.columns[:2]

for index, ax in enumerate(axes.flat):
    axes[index].plot(freqs, amplitudes_back[:, index])
    axes[index].set_xlim(0, 8)
    axes[index].set(ylabel=f'Amplitude {names[index]}')

axes[index].set(xlabel='Frequency (Hz)');

show()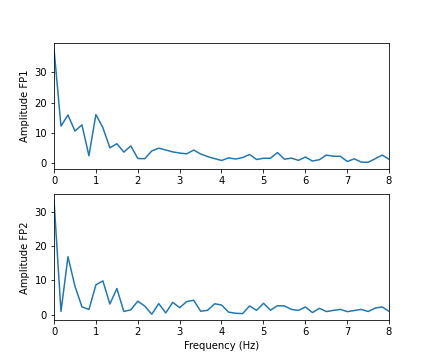

We can see that in these two channels, the main amplitude contributions lie in the low frequencies, below 2 Hz.

Let us compare the corresponding figure for the case of seizure activity:

PYTHON 

data_epil_fft = fft(data_epil, axis=0)

PYTHON 

fig, axes = subplots(figsize=(6, 5), ncols=1, nrows=no_win, sharex=False)

names = df_epil.columns[:2]

amplitudes_epil = (2.0 / rows) * abs(data_epil_fft[:rows//2, :2])

for index, ax in enumerate(axes.flat):
    axes[index].plot(freqs, amplitudes_epil[:, index])
    axes[index].set_xlim(0, 12)
    axes[index].set(ylabel=f'Amplitude {names[index]}')

axes[index].set(xlabel='Frequency (Hz)');

show()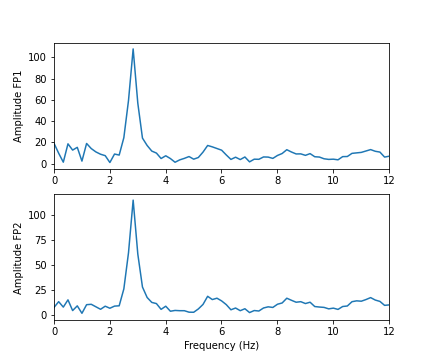
The main frequency of the epileptic rhythm is between 2 and 3 Hz.

As we can see above in the Fourier spectra above, the amplitudes are high for low frequencies and tend to decrease with increasing frequency. Sometimes it is useful to see the high frequencies enhanced. This can be achieved with a logarithmic plot of the powers.

PYTHON 

fig, axes = subplots(figsize=(6, 6), ncols=1, nrows=no_win, sharex=False)

for index, ax in enumerate(axes.flat):

    axes[index].plot(freqs, amplitudes_back[:, index])
    axes[index].set_xlim(0, 30)
    axes[index].set(ylabel=f'Amplitude {names[index]}')
    axes[index].set_yscale('log')

axes[no_win-1].set(xlabel='Frequency (Hz)');
fig.suptitle('Logarithmic Fourier Spectra of Background EEG', fontsize=16);

show()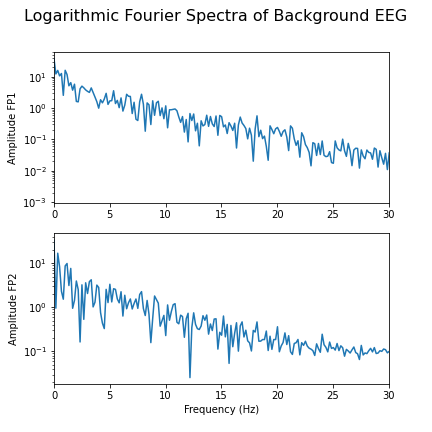

And for the seizure data:

PYTHON 

fig, axes = subplots(figsize=(6, 10), ncols=1, nrows=no_win, sharex=False)

for index, ax in enumerate(axes.flat):

    axes[index].plot(freqs, amplitudes_epil[:, index])
    axes[index].set_xlim(0, 30)
    axes[index].set(ylabel=f'Power {names[index]}')
    axes[index].set_yscale('log')

axes[no_win-1].set(xlabel='Frequency (Hz)');
fig.suptitle('Logarithmic Fourier Spectra of Seizure EEG', fontsize=16);

show()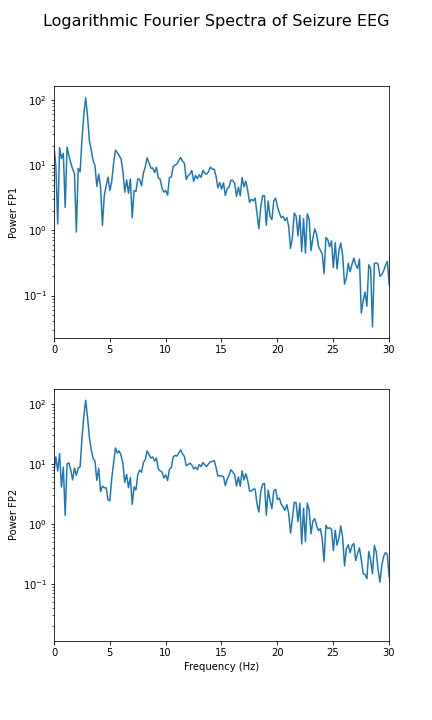

In the spectrum of the absence data, it is now more obvious that there are further maxima at 6, 9, 12, and perhaps 15Hz. These are integer multiples or ‘harmonics’ of the basic frequency at around 3Hz, also referred to as the fundamental frequency.

A feature that can be used as a summary statistic, is to caclulate the band power for each channel. The band power can be obtained as the sum of all powers within a specified range of frequencies, also called the ‘band’. The band power thus represents a single number.

DIY2: Fourier spectra of filtered data

Calculate and display the Fourier spectra of the first two channels filtered between 4 and 12 Hz for the absence seizure data. Can you find harmonics?

PYTHON 

data_epil_filt = data_filter(data_epil, sr, 4, 12)

data_epil_fft = fft(data_epil_filt, axis=0)

rows = data_epil.shape[0]

freqs = (sr/2)*linspace(0, 1, int(rows/2))

amplitudes_epil = (2.0 / rows) * abs(data_epil_fft[:rows//2, :no_win])

fig, axes = subplots(figsize=(6, 10), ncols=1, nrows=no_win, sharex=False)

for index, ax in enumerate(axes.flat):
    axes[index].plot(freqs, amplitudes_epil[:, index])
    axes[index].set_xlim(0, 12)
    axes[index].set(ylabel=f'Amplitudes {names[index]}')
axes[no_win-1].set(xlabel='Frequency (Hz)');

fig.suptitle('Fourier Spectra of Seizure EEG', fontsize=16);

show()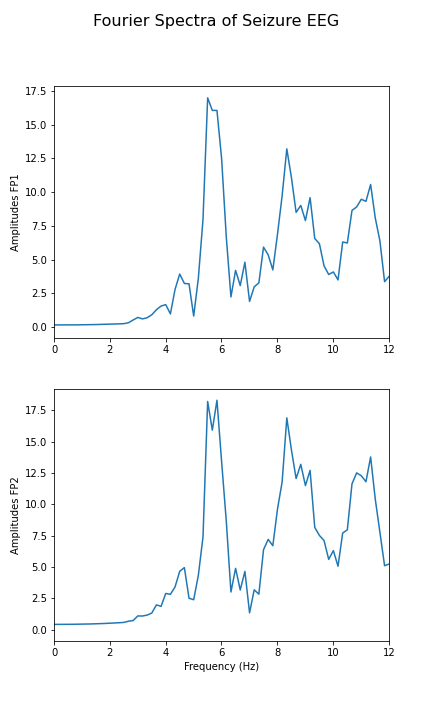

Figure 8

Figure 9

Figure 10

Figure 11

Figure 12

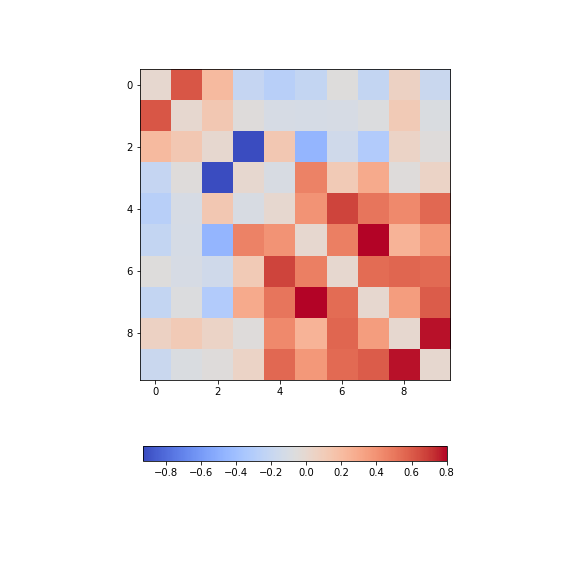
Figure 13

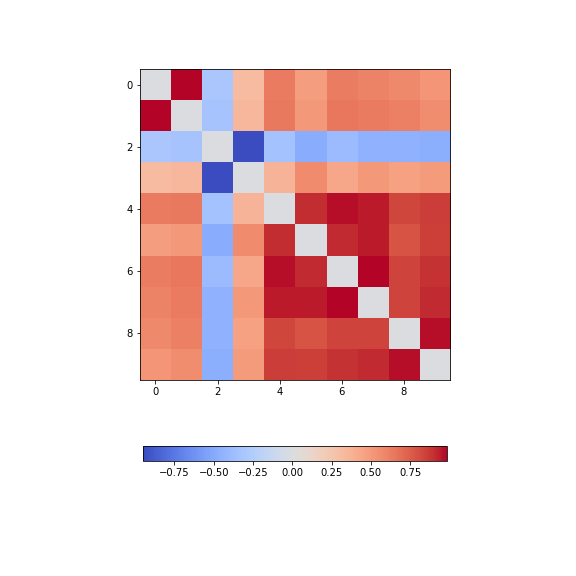
Figure 14

Figure 15

Figure 16

Figure 17

Figure 18

### Q5 ### Correlation Matrix

Figure 19

Figure 20

Figure 21

Figure 22