Content from Classification

---

Last updated on 2024-11-04 | Edit this page

Download Chapter PDF

Download Chapter notebook (ipynb)

Mandatory Lesson Feedback Survey

Overview

Questions

• How to prepare data for classification?
• Why do we need to train a model?
• What does a state space plot represent?
• How to obtain prediction probabilities?
• What are the important features?

Objectives

• Understanding the classification challenge.
• Training a classifier model.
• Understanding the state space plot of model predictions.
• Obtaining prediction probabilities.
• Finding important features.

Prerequisite

• Data Handling
• Numpy arrays (see accompanying tutorial)
• Basic Matplotlib plotting

Import functions

PYTHON

from pandas import read_csv

from numpy import arange, asarray, linspace, c_, meshgrid, zeros, ones

from numpy.random import uniform, seed

from matplotlib.pyplot import subplots, scatter, xlabel, ylabel, xticks, show

Example: Visual Classification

---

Import the ‘patients_data’ toy dataset and scatter the data for Height and Weight.

PYTHON

# Please adjust your path to the file
df = read_csv('data/patients_data.csv')

print(df.shape)

# Convert inches to cm and pounds to kg:
df['Height'] = 2.540*df['Height']
df['Weight'] = 0.454*df['Weight']

df.head(10)

OUTPUT

(100, 7)
   Age  Height  Weight  Systolic  Diastolic  Smoker  Gender
0   38  180.34  79.904       124         93       1    Male
1   43  175.26  74.002       109         77       0    Male
2   38  162.56  59.474       125         83       0  Female
3   40  170.18  60.382       117         75       0  Female
4   49  162.56  54.026       122         80       0  Female
5   46  172.72  64.468       121         70       0  Female
6   33  162.56  64.468       130         88       1  Female
7   40  172.72  81.720       115         82       0    Male
8   28  172.72  83.082       115         78       0    Male
9   31  167.64  59.928       118         86       0  Female

Note that data in the first five columns are either integers (age) or real numbers (floating point). The classes (categorical data) in the last two columns come as binary (0/1) for ‘smokers/non-smokers’ and as strings for ‘male/female’. Both can be used for classification.

The classification challenge

I am given a set of data from a single subject and feed them to a computational model. The model then predicts to what (predefined) class this subject belongs. Example: given height and weight data, the model might try to predict whether the subject is a smoker or a non-smoker. A naive model will, of course, not be able to predict reasonably. The supervised approach in machine learning is to provide the model with a set of data where the class has been verified beforehand and the model can test its (initially random) predictions against the provided class. An optimisation algorithm is then run to adjust the (internal) model setting such that the predictions improve as much as possible. When no further improvement is achieved, the algorithm stops. The model is then trained and ready to predict.

The act of classification is to assign labels to unlabelled data after model exposure to previously labelled data (e.g. based on medical knowledge in the case of disease data).

In contrast, in unsupervised machine learning the assignment is done based on exposure to unlabelled data following a search for distinctive features or ‘structure’ in the data.

We can first check if we are able to distinguish classes visually. For this, we scatter the data of two columns of a dataframe using the column names. That is, we look at the distribution of points in a plane. Then we use the class label to color each point in the plane according to the class it belongs to. String labels like ‘male’ / ‘female’ first need to be converted to Boolean (binary). 0/1 labels as in the ‘smokers/non-smokers’ column can be used directly.

Let us plot the height-weight data and label them for both cases.

PYTHON

fig, ax = subplots(figsize=(12,6),ncols=2,nrows=1)

gender_boolean = df['Gender'] == 'Female'

ax[0].scatter(df['Height'], df['Weight'], c=gender_boolean, cmap='bwr')
ax[0].set_xlabel('Height', fontsize=14)
ax[0].set_ylabel('Weight', fontsize=14)
ax[0].set_title('Female (red), Male (blue)', fontsize=16)

ax[1].scatter(df['Height'], df['Weight'], c=df['Smoker'], cmap='bwr')
ax[1].set_xlabel('Height', fontsize=16)
ax[1].set_ylabel('Weight', fontsize=16)
ax[1].set_title('Smoker (red), Non-Smoker (blue)', fontsize=16);

show()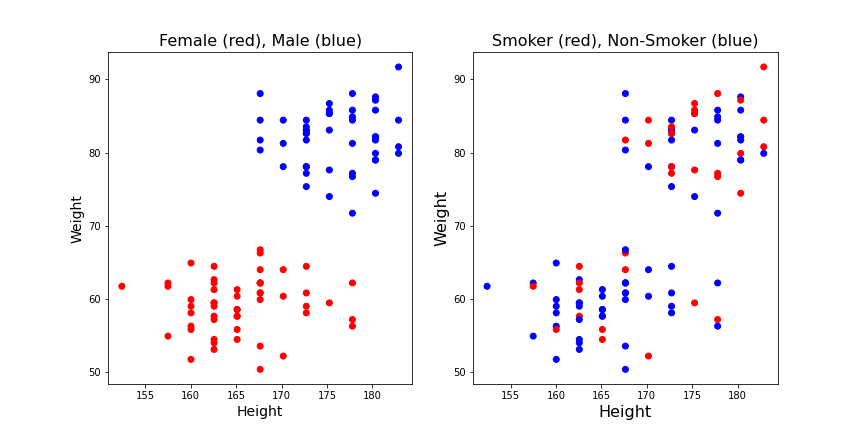

It appears from these graphs that based on height and weight data it is possible to distinguish male and female. Based on visual inspection one could conclude that everybody with a weight lower than 70kg is female and everybody with a weight above 70kg is male. That would be a classification based on the weight alone. It also appears that the data points classified as ‘male’ are taller on average, so it might be helpful to have the height recorded as well. E.g it could improve the prediction of gender for new subjects with a weight around 70 kg. But it would not be the best choice if only a single quantity was used. Thus, a second conclusion is that based on these data the weight is more important for the classification than the height.

On the other hand, based on the smoker / non-smoker data it will not be possible to distinguish smokers from non-smokers. Red dots and blue dots are scattered throughout the graph. The conclusion is that height and weight cannot be used to predict whether a subject is a smoker.

Supervised Learning: Training a Model

---

This lesson deals with labelled data. Labelled data are numerical data with an extra column of a label for each sample. A sample can consist of any number of individual observations but must be at least two.

Examples of labels include ‘control group / test group’; ‘male / female’; ‘healthy / diseased’; ‘before treatment / after treatment’.

The task in Supervised Machine Learning is to fit (train) a model to distinguish between the groups by ‘learning’ from so-called training data. After training, the optimised model automatically labels incoming (unlabeled) data. The better the model, the better the labelling (prediction).

The model itself is a black box. It has set default parameters to start with and thus performs badly in the beginning. Essentially, it starts by predicting a label at random. The process of training consists in repeatedly changing the model parameters such that the performance improves. After the training, the model parameters are supposed to be optimal. Of course, the model cannot be expected to reveal anything about the mechanism or cause that underlies the distinction between the labels.

The performance of the model is tested by splitting a dataset with labels into:

• the train data, those that will be used for model fitting, and

• the test data, those that will be used to check how well the model predicts.

The result of the model fitting is then assessed by checking how many of the (withheld) labels in the test data were correctly predicted by the trained model. We can also retrieve the confidence of the model prediction, i.e. the probability that the assigned label is correct.

As an additional result, the procedure will generate the so-called feature importances: similar to how we concluded above that weight is more important than height for gender prediction, the feature importance informs to which degree each of the data columns actually contributes to the predictions.

Scikit Learn

---

We will import our machine learning functionality from the SciKit Learn library.

SciKit Learn

SciKit Learn is a renowned open source application programming interface (API) for machine learning. It enjoys a vibrant community and is well maintained. It is always beneficial to use the official documentations for every API. SciKit Learn provides an exceptional documentation with detailed explanations and examples at every level.

The implementation of algorithms in SciKit Learn follows a very specific protocol. First and foremost, it uses a programming paradigm known as object-oriented programming (OOP). Thanks to Python, this does not mean that you as the user are also forced to use OOP. But you need to follow a specific protocol to use the tools that are provided by SciKit Learn.

Unlike functions that perform a specific task and return the results, in OOP, we use classes to encapsulate interconnected components and functionalities. In accordance with the convention of best practices for Python programming (also known as PEP8), classes are implemented with camel-case characters; e.g. RandomForestClassifier. In contrast, functions should be implemented using lower-case characters only; e.g. min or round.

Classification

---

Prepare data with labels

The terminology that is widely used in Machine Learning (including Scikit Learn) refers to data points as samples, and the different types of recordings(columns in our case) are referred to as features. In Numpy notation, samples are organised in rows, features in columns.

We can use the function uniform from numpy.random to generate uniformly distributed random data. Here we create 100 samples of two features (as in the visualisation above). We decide to have values distributed between 0 and 100.

The convention in machine learning is to call the training data ‘X’. This array must be two dimensional, where rows are the samples and columns are the features.

PYTHON

low  = 0
high = 100

n_samples, m_features = 100, 2

RANDOM_SEED  = 1234

seed(RANDOM_SEED)

random_numbers = uniform(low=low, high=high, size=(n_samples, m_features))

X = random_numbers.round(3)

print('Dimensions of training data')
print('')
print('Number of samples:  ', X.shape[0])
print('Number of features: ', X.shape[1])
print('')

OUTPUT

Dimensions of training data

Number of samples:   100
Number of features:  2

Note

This code uses a random number generator. The output of a random number generator is different each time it is run. On the one hand, this is good because it allows us to create many realisations of samples drawn from a fixed distribution. On the other hand, when testing and sharing code this prevents exact reproduction of results. We therefore use the seed function to reset the generator such that with a given number for the seed (the parameter called RANDOM_SEED) the same numbers are produced.

Let us check the histograms of both features:

PYTHON

fig, ax = subplots()

ax.hist(X, bins=10);

show()

We find that both features are distributed over the selected range of values. Due to the small number of samples, the distribution is not very even.

The categorical data used to distinguish between different classes are called labels. Let us create an artificial set of labels for our first classification task.

We pick an arbitrary threshold and call all values True if the values in both the first and the second feature are above the threshold. The resulting labels True and False can be viewed as 0/1 using the method astype with argument int.

PYTHON

threshold = 50

y = (X[:,0] > threshold) & (X[:,1] > threshold)

y.astype(int)

OUTPUT

array([0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0,
       1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1,
       0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
       0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1])

If both features (columns) were risk factors, this might be interpreted as: only if both risk factors are above the threshold, a subject is classified as ‘at risk’, meaning it gets label ‘True’ or ‘1’.

Labels must be one-dimensional. You can check this by printing the shape. The output should be a single number:

PYTHON

print('Number of labels:', y.shape)

OUTPUT

Number of labels: (100,)

The Random Forest Classifier

To start with our learning algorithm, we import one of the many classifiers from Scikit Learn: it is called Random Forest.

PYTHON

from sklearn.ensemble import RandomForestClassifier

The Random Forest is a member of the ensemble learning family, whose objective is to combine the predictions of several optimisations to improve their performance, generalisability, and robustness.

Ensemble methods are often divided into two different categories:

1. Averaging methods: Build several estimators independently, and average their predictions. In general, the combined estimator tends to perform better than any single estimator due to the reduction in variance. Examples: Random Forest and Decision Tree.

2. Boosting methods: Build the estimators sequentially, and attempt to reduce the bias of the combined estimator. Although the performance of individual estimators may be weak, upon combination, they amount to a powerful ensemble. Examples: Gradient Boosting and AdaBoost.

We now train a model using the Python class for the Random Forest classifier. Unlike a function (which we can use out of the box) a class needs to be instantiated before it can be used. In Python, we instantiate a class as follows:

PYTHON

clf = RandomForestClassifier(random_state=RANDOM_SEED)

where clf now represents an instance of class RandomForestClassifier. Note that we have set the keyword argument random_state to a number. This is to assure reproducibility of the results. (It does not have to be the same as above, pick any integer).

The instance of a class is typically referred to as an object, whose type is the class that it represents:

PYTHON

print('Type of clf:', type(clf))
print('')

OUTPUT

Type of clf: <class 'sklearn.ensemble._forest.RandomForestClassifier'>

Once instantiated, we can use this object, clf, to access the methods that are associated with that class. Methods are essentially functions that are encapsulated inside a class.

In SciKit Learn all classes have a .fit() method. Its function is to receive the training data and perform the training of the model.

Train a model

To train a model, we apply the fit method to the training data, labelled ‘X’, given the corresponding labels ‘y’:

PYTHON

clf.fit(X, y)

RandomForestClassifier(random_state=1234)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

And that’s it. All the machine learning magic done. clf is now a trained model with optimised parameters which we can use to predict new data.

Predict Test Data

Categorical Prediction

We start by creating a number of test data in the same way as we created the training data. Note that the number of test samples is arbitrary. You can create any number of samples. However, you must provide the same number of features (columns) used in the training of the classifier. In our case that is 2.

PYTHON

RANDOM_SEED_2 = 123

seed(RANDOM_SEED_2)

new_samples = 10

features = X.shape[1]

new_data = uniform(low=low, high=high, size=(10, 2))

print('Shape of new data', new_data.shape)
print('')
print(new_data)

OUTPUT

Shape of new data (10, 2)

[[69.64691856 28.6139335 ]
 [22.68514536 55.13147691]
 [71.94689698 42.31064601]
 [98.07641984 68.48297386]
 [48.09319015 39.21175182]
 [34.31780162 72.90497074]
 [43.85722447  5.96778966]
 [39.80442553 73.79954057]
 [18.24917305 17.54517561]
 [53.15513738 53.18275871]]

There are 10 randomly created pairs of numbers in the same range as the training data. They represent ‘unlabelled’ incoming data which we offer to the trained model.

The method .predict() helps us to find out what the model claims these data to be:

PYTHON

predictions = clf.predict(new_data)

print('Predictions: ', predictions)

OUTPUT

Predictions:  [False False False  True False False False False False  True]

They can also be viewed as zeros and ones:

PYTHON

predictions.astype(int)

OUTPUT

array([0, 0, 0, 1, 0, 0, 0, 0, 0, 1])

According to the model, data points with indices 3, and 9 are in class True (or 1).

Predicting individual samples is fine, but does not tell us whether the classifier was able to create a good model of the class distinction. To check the training result systematically, we create a state space grid over the state space. This is the same as creating a coordinate system of data points (as in a scatter plot), in our case with values from 0 to 100 in each feature.

Here we use a resolution of 100, ie. we create a 100 by 100 grid:

PYTHON

resolution = 100

vec_a = linspace(low, high, resolution)
vec_b = vec_a

grid_a, grid_b = meshgrid(vec_a, vec_b)

grid_a_flat = grid_a.ravel()
grid_b_flat = grid_b.ravel()

XY_statespace = c_[grid_a_flat, grid_b_flat]

print(XY_statespace.shape)

OUTPUT

(10000, 2)

Now we can offer the grid of the X-Y state space as ‘new data’ to the classifier and obtain the predictions. We can then plot the grid points and colour them according to the labels assigned by the trained model.

PYTHON

predictions = clf.predict(XY_statespace)

predictions.shape

OUTPUT

(10000,)

We obtain 10,000 predictions, one for each point on the grid.

To compare the data with the original thresholds and the model predictions we can use plots of the state space:

PYTHON

feature_1, feature_2 = 0, 1

fig, ax = subplots(ncols=2, nrows=1, figsize=(10, 5))

ax[0].scatter(X[:, feature_1], X[:, feature_2], c=y, s=4, cmap='bwr');
ax[1].scatter(XY_statespace[:, feature_1], XY_statespace[:, feature_2], c=predictions, s=1, cmap='bwr');

p1, p2 = [threshold, threshold], [100, threshold]
p3, p4 = [threshold, 100], [threshold, threshold]

ax[0].plot(p1, p2, c='k')
ax[0].plot(p3, p4, c='k')

ax[0].set_xlabel('Feature 1', fontsize=16)
ax[0].set_ylabel('Feature 2', fontsize=16);
ax[1].set_xlabel('Feature 1', fontsize=16);

show()

Left is a scatter plot of the data points used for training. They are coloured according to their labels. The black lines indicate the threshold boundaries that we introduced to distinguish the two classes. On the right hand side are the predictions for the coordinate grid. Label 0 is blue, label 1 is red.

Based on the training samples (left), a good classification can be achieved with the model (right). But some problems persist. In particular, the boundaries are not sharp.

Probability Prediction

Let us pick a sample near the boundary. We can get its predicted label. In addition, using .predict_proba() we can get the probability of this prediction. This reflects the confidence in the prediction. 50% probability means, the prediction is at chance level, i.e. equivalent to a coin toss.

PYTHON

pos = 55

test_sample = [[pos, pos]]

test_sample_label = clf.predict(test_sample)

test_sample_proba = clf.predict_proba(test_sample)

print('Prediction:', test_sample_label)
print(clf.classes_, test_sample_proba)

OUTPUT

Prediction: [False]
[False  True] [[0.57 0.43]]

PYTHON

bins = arange(test_sample_proba.shape[1])

fig, ax = subplots()

ax.bar(bins, test_sample_proba[0,:], color=('b', 'r'))
ax.set_ylabel('Probability', fontsize=16)
xticks(bins, ('Label 0', 'Label 1'), fontsize=16);

show()

Even though the sample is from the region that (according to the creation of the data) is in the ‘True’ region, it is labelled as false. The reason is that there were few or no training data points in that specific region.

Here is a plot of the probability for the state space. White represents False and Black represents True, the values in between are gray coded. Note that the probability values are complementary. We only need the probabilities for one of our classes.

PYTHON

state_space_proba = clf.predict_proba(XY_statespace)

grid_shape = grid_a.shape

proba_grid = state_space_proba[:, 1].reshape(grid_shape)

contour_levels = linspace(0, 1, 6)


fig, ax = subplots(figsize=(6, 5))

cax = ax.contourf(grid_a, grid_b, proba_grid, cmap='Greys', levels=contour_levels)
fig.colorbar(cax)

ax.scatter(test_sample[0][0], test_sample[0][1], c='r', marker='o', s=100)

ax.plot(p1, p2, p3, p4, c='r')

ax.set_xlabel('Feature 1', fontsize=16)
ax.set_ylabel('Feature 2', fontsize=16);

show()

The single red dot marks the individual data point we used to illustrate the prediction probability above.

Feature Importances

We can check the contribution of each feature for the success of the classification. The feature importance is given as the fraction contribution of each feature to the prediction.

PYTHON

importances = clf.feature_importances_

print('Relative importance:')

template = 'Feature 1: {:.1f}%; Feature 2: {:.1f}%'

print(template.format(importances[0]*100, importances[1]*100))

bins = arange(importances.shape[0])

fig, ax = subplots()

ax.bar(bins, importances, color=('g', 'm'));
ax.set_ylabel('Feature Importance', fontsize=16)

xticks(bins, ('Feature 1', 'Feature 2'), fontsize=16);

show()

OUTPUT

Relative importance:
Feature 1: 61.6%; Feature 2: 38.4%

In this case, the predictions are based on a 61% contribution from feature 1 and a 38% contribution from feature 2.

Application

---

Now we pick the ‘Height’ and ‘Weight’ columns from the patients data to predict the gender labels. We use a split of 4/5 of the data for training and 1/5 for testing.

PYTHON

df = read_csv('data/patients_data.csv')

print(df.shape)

# Convert pounds to kg and inches to cm:
df['Weight'] = 0.454*df['Weight']
df['Height'] = 2.540*df['Height']

df.head(10)

OUTPUT

(100, 7)
   Age  Height  Weight  Systolic  Diastolic  Smoker  Gender
0   38  180.34  79.904       124         93       1    Male
1   43  175.26  74.002       109         77       0    Male
2   38  162.56  59.474       125         83       0  Female
3   40  170.18  60.382       117         75       0  Female
4   49  162.56  54.026       122         80       0  Female
5   46  172.72  64.468       121         70       0  Female
6   33  162.56  64.468       130         88       1  Female
7   40  172.72  81.720       115         82       0    Male
8   28  172.72  83.082       115         78       0    Male
9   31  167.64  59.928       118         86       0  Female

Prepare training data and labels

PYTHON

# Extract data as numpy array
df_np = df.to_numpy()

# Pick a fraction of height and weight data as training data
samples = 80

X = df_np[:samples, [1, 2]]

print(X.shape)

OUTPUT

(80, 2)

For the labels of the training data we convert the ‘Male’ and ‘Female’ strings to categorical values.

PYTHON

gender_boolean = df['Gender'] == 'Female'

y = gender_boolean[:80]

# printed as 0 and 1:

y.astype('int')

OUTPUT

0     0
1     0
2     1
3     1
4     1
     ..
75    0
76    1
77    0
78    0
79    1
Name: Gender, Length: 80, dtype: int64

Train classifier and predict

PYTHON

from sklearn.ensemble import RandomForestClassifier

seed(RANDOM_SEED)

clf = RandomForestClassifier(random_state=RANDOM_SEED)

clf.fit(X, y)

RandomForestClassifier(random_state=1234)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We now take the remaining fifth of the data to predict.

PYTHON

X_test = df.loc[80:, ['Height', 'Weight']]

X_test = X_test.values

predict_test = clf.predict(X_test)

probab_test = clf.predict_proba(X_test)

print('Predictions: ', predict_test, '\n', 'Probabilities: ', '\n',  probab_test)

OUTPUT

Predictions:  [False False False  True  True False  True  True  True  True False False
  True False  True False False False False False]
 Probabilities:
 [[1.   0.  ]
 [1.   0.  ]
 [1.   0.  ]
 [0.   1.  ]
 [0.   1.  ]
 [1.   0.  ]
 [0.   1.  ]
 [0.   1.  ]
 [0.   1.  ]
 [0.   1.  ]
 [1.   0.  ]
 [1.   0.  ]
 [0.02 0.98]
 [1.   0.  ]
 [0.   1.  ]
 [1.   0.  ]
 [1.   0.  ]
 [1.   0.  ]
 [1.   0.  ]
 [0.97 0.03]]

As in the example above, we create a state space grid to visualise the outcome for the two features.

PYTHON

X1_min, X1_max = min(X[:, 0]), max(X[:, 0])
X2_min, X2_max = min(X[:, 1]), max(X[:, 1])

resolution = 100

vec_a = linspace(X1_min, X1_max, resolution)
vec_b = linspace(X2_min, X2_max, resolution)

grid_a, grid_b = meshgrid(vec_a, vec_b)


grid_a_flat = grid_a.ravel()
grid_b_flat = grid_b.ravel()

X_statespace = c_[grid_a_flat, grid_b_flat]

We can now obtain the categorical and probability predictions from the trained classifier for all points of the grid.

PYTHON

predict = clf.predict(X_statespace)
probabs = clf.predict_proba(X_statespace)

Here is the plot of the state space and the predicted probabilities:

PYTHON

feature_1, feature_2 = 0, 1

fig, ax = subplots(ncols=3, nrows=1, figsize=(15, 5))

ax[0].scatter(X[:, feature_1], X[:, feature_2], c=y, s=40, cmap='bwr');
ax[0].set_xlim(X1_min, X1_max);
ax[0].set_ylim(X2_min, X2_max);
ax[0].set_xlabel('Feature 1', fontsize=16);
ax[0].set_ylabel('Feature 2', fontsize=16);

cax1 = ax[1].scatter(X_statespace[:, feature_1], X_statespace[:, feature_2], c=predict, s=1, cmap='bwr');
ax[1].scatter(X_test[:, feature_1], X_test[:, feature_2], c=predict_test, s=40, cmap='Greys');
ax[1].set_xlabel('Feature 1', fontsize=16);
ax[1].set_xlim(X1_min, X1_max);
ax[1].set_ylim(X2_min, X2_max);
fig.colorbar(cax1, ax=ax[1]);

grid_shape = grid_a.shape

probab_grid = probabs[:, 1].reshape(grid_shape)

# Subject with 170cm and 70 kg
pos1, pos2 = 170, 70

test_sample = [pos1, pos2]

contour_levels = linspace(0, 1, 10)

cax2 = ax[2].contourf(grid_a, grid_b, probab_grid, cmap='Greys', levels=contour_levels);
fig.colorbar(cax2, ax=ax[2]);

ax[2].scatter(test_sample[0], test_sample[1], c='r', marker='o', s=100);
ax[2].set_xlabel('Feature 1', fontsize=16);
ax[2].set_xlim(X1_min, X1_max);
ax[2].set_ylim(X2_min, X2_max);

show()

The left panel shows the original data with labels as colours, i.e. the training data. Central panel shows the classified state space with the test samples as black dots in predicted category ‘Female’ and white dots in predicted category ‘Male’. Right panel shows the state space with prediction probabilities with black for ‘Female’ and white for ‘Male’. The red dot represents the simulated subject with 170cm and 70 kg (see below).

Probability of a single observation

Let us pick that subject and obtain its predicted label and probability. Note the use of double brackets to create a sample that is a two-dimensional array.

PYTHON

test_sample = [[pos1, pos2]]

test_predict = clf.predict(test_sample)
test_proba   = clf.predict_proba(test_sample)

print('Predicted class:', test_predict, 'Female')
print('Probability:', test_proba[0, 0])
print('')

bins = arange(test_proba.shape[1])

fig, ax = subplots()

ax.bar(bins, test_proba[0,:], color=('r', 'b'));
xticks(bins, ('Female', 'Male'), fontsize=16);
ax.set_ylabel('Probability', fontsize=16);

show()

OUTPUT

Predicted class: [False] Female
Probability: 0.66

This shows that the predicted label is female but the probability is less than 70 % and, e.g. if a clinical decision was to be taken based on the outcome of the classification, it might suggest looking for additional evidence before the decision is made.

Feature Importances

PYTHON

importances = clf.feature_importances_

print('Features importances:')
template = 'Feature 1: {:.1f}%; Feature 2: {:.1f}%'
print(template.format(importances[0]*100, importances[1]*100))
print('')

bins = arange(importances.shape[0])

fig, ax = subplots()

ax.bar(bins, importances, color=('m', 'g'));
xticks(bins, ('Feature 1', 'Feature 2'), fontsize=16);
ax.set_ylabel('Feature Importance', fontsize=16);

show()

OUTPUT

Features importances:
Feature 1: 31.7%; Feature 2: 68.3%

Feature Height contributes about one third and feature Weight about two thirds to the decisions.

Feature importances can be used in data sets with many features, e.g. to reduce the number of features used for classification. Some features might not contribute to the classification and could therefore be left out of the process.

In the next lesson, we are going to test multiple classifiers and quantify their performance to improve the outcome of the classification.

Exercises

---

End of chapter Exercises

Repeat the training and prediction workflow as above for two other features in the data, namely: Systole and Diastole values. Use 70 training and 30 testing samples where the labels are assigned according to the condition: 0 if ‘non-smoker’, 1 if ‘smoker’.

Use the above code to:

1. Train the random forest classifier.

2. Create state space plots with scatter plot, categorical colouring, and probability contour plot.

3. Compare the predicted and actual labels to check how well the trained model performed: how many of the 30 test data points are correctly predicted?

4. Plot the feature importance to check how much the systolic and diastolic values contributed to the predictions.

Solutions will be provided once the submitted assignments are marked and returned.

Further Practice: Iris data

You can try to use the Random Forest classifier on the Iris data:

The Iris data are a collection of five features (sepal length, sepal width, petal length, petal width and species) from 3 species of Iris (Iris setosa, Iris virginica and Iris versicolor). The species name is used for training in classification.

Import the data from scikit-learn as:

PYTHON

from sklearn import datasets

# Import Iris data
iris = datasets.load_iris()

# Get first two features and labels
X = iris.data[:, :2]
y = iris.target

print(X.shape, y.shape)

OUTPUT

(150, 2) (150,)

Key Points

• Classification is to assign labels to unlabeled data.
• SciKit Learn is an open source application programming interface (API) for machine learning.
• .fit() function is used to receive the training data and perform the training of the model.
• .predict() function helps to find out what the model claims these data to be.
• .predict_proba() function predicts the probability of any predictions.

Content from Improvement

---

Last updated on 2024-08-06 | Edit this page

Download Chapter PDF

Download Chapter notebook (ipynb)

Mandatory Lesson Feedback Survey

Overview

Questions

• How to deal with complex classification problems?
• Why is it important to use different classification algorithms?
• What is the best way to find the optimal classifier?
• How can we avoid over-fitting of data?
• How do we evaluate the performance of classifiers?

Objectives

• Understanding complex training and testing data.
• Comparison of different model classes.
• Explaining the stratified shuffle split.
• Evaluation of classification - the ROC and AUC curves.

Remarks

1. From now on the code will become more complex. When copied, the code should run without errors with the given data sets. (Please report any errors thrown when running the code without modifications).

2. Make a copy of the notebook and start experimenting by modifying part of the code and comparing the outcome. Modifying existing code is one of the successful strategies when learning to programme as a non-programmer.

3. The first resource to consult when facing bugs are the official documentations, be it Python, Numpy, SciKit Learn or other.

4. If you formulate a problem adequately, often there may be good answers on Stack Overflow.

5. Sometimes, simply copying and pasting an error message into the search engine can point you to the solution.

Import functions

PYTHON

from numpy import mgrid, linspace, c_, arange, mean, array
from numpy.random import uniform, seed

from mpl_toolkits import mplot3d
from matplotlib.pyplot import subplots, axes, scatter, xticks, show

from sklearn.datasets import make_circles

Challenge

We would like to test several machine learning models’ ability to deal with a complicated task. A complicated task is one where the topology of the labelled data is not trivially separable into classes by (hyper)planes, e.g. by a straight line in a scatter plot.

Our example is one class of data organised in a doughnut shape and the other class contained within the first doughnut forming a doughnut-within-a-doughnut.

Here is the function code to create these data, followed by a function call to produce a figure.

PYTHON

def make_torus_3D(n_samples=100, shuffle=True, noise=None, random_state=None,
                 factor=.8):
    """Make a large torus containing a smaller torus in 3d.

    A toy dataset to visualize clustering and classification
    algorithms.

    Read more in the :ref:`User Guide <sample_generators>`.

    Parameters
    ----------
    n_samples : int, optional (default=100)
        The total number of points generated. If odd, the inner circle will
        have one point more than the outer circle.

    shuffle : bool, optional (default=True)
        Whether to shuffle the samples.

    noise : double or None (default=None)
        Standard deviation of Gaussian noise added to the data.

    random_state : int, RandomState instance or None (default)
        Determines random number generation for dataset shuffling and noise.
        Pass an int for reproducible output across multiple function calls.
        See :term:`Glossary <random_state>`.

    factor : 0 < double < 1 (default=.8)
        Scale factor between inner and outer circle.

    Returns
    -------
    X : array of shape [n_samples, 2]
        The generated samples.

    y : array of shape [n_samples]
        The integer labels (0 or 1) for class membership of each sample.
    """
    from numpy import pi, linspace, cos, sin, append, ones, zeros, hstack, vstack, intp
    from sklearn.utils import check_random_state, shuffle

    if factor >= 1 or factor < 0:
        raise ValueError("'factor' has to be between 0 and 1.")

    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out

    co, ao, ci, ai = 3, 1, 3.6, 0.2
    generator = check_random_state(random_state)
    # to not have the first point = last point, we set endpoint=False
    linspace_out = linspace(0, 2 * pi, n_samples_out, endpoint=False)
    linspace_in  = linspace(0, 2 * pi, n_samples_in,  endpoint=False)
    outer_circ_x = (co+ao*cos(linspace_out)) * cos(linspace_out*61.1)
    outer_circ_y = (co+ao*cos(linspace_out)) * sin(linspace_out*61.1)
    outer_circ_z =    ao*sin(linspace_out)

    inner_circ_x = (ci+ai*cos(linspace_in)) * cos(linspace_in*61.1)* factor
    inner_circ_y = (ci+ai*cos(linspace_in)) * sin(linspace_in*61.1) * factor
    inner_circ_z =    ai*sin(linspace_in) * factor

    X = vstack([append(outer_circ_x, inner_circ_x),
                append(outer_circ_y, inner_circ_y),
                append(outer_circ_z, inner_circ_z)]).T

    y = hstack([zeros(n_samples_out, dtype=intp),
                   ones(n_samples_in, dtype=intp)])

    if shuffle:
        X, y = shuffle(X, y, random_state=generator)

    if noise is not None:
        X += generator.normal(scale=noise, size=X.shape)

    return X, y

PYTHON

RANDOM_STATE  = 12345
seed(RANDOM_STATE)

X, y = make_torus_3D(n_samples=2000, factor=.9, noise=.001, random_state=RANDOM_STATE)

feature_1, feature_2, feature_3 = 0, 1, 2
ft_min, ft_max = X.min(), X.max()

fig, ax = subplots(figsize=(12, 9))

ax = axes(projection="3d")

im = ax.scatter3D(X[:, feature_1], X[:, feature_2], X[:, feature_3], marker='o', s=20, c=y, cmap='bwr');

ax.set_xlabel('Feature 1')
ax.set_ylabel('Feature 2')
ax.set_zlabel('Feature 3')

# Angles to pick the perspective
ax.view_init(30, 50);

show()

The challenge here is that the only way to separate the data of the two labels from each other is to find a separating border that lies between the blue and the red doughnut (mathematically: torus) and itself is a torus, i.e. a complex topology. Similarly, one can test to separate one class of data that lie on the surface of a sphere and then have data on another sphere embedded within it. Typically, it is unknown what type of high-dimensional topologies is present in biological data. As such it is not clear at the outset which classification strategy will work best. Let us start with a simpler example.

Traing a variety of machine learning models

---

SciKit Learn provides the means to generate practice datasets with specific qualities. In this section, we will use the make_circles function. (see the documentations):

Circular Test Data

PYTHON

RANDOM_STATE  = 1234
seed(RANDOM_STATE)

X, y = make_circles(n_samples=500, factor=0.3, noise=.05, random_state=RANDOM_STATE)

feature_1, feature_2 = 0, 1
ft_min, ft_max = X.min(), X.max()

print('Shape of X:', X.shape)

OUTPUT

Shape of X: (500, 2)

PYTHON

fig, ax = subplots(figsize=(10, 5), nrows=1, ncols=2)
ax[0].scatter(X[:, feature_1], X[:, feature_2], c=y, s=4, cmap='bwr');
ax[1].hist(X);

show()

The function yields only two features. The reason is that with two features we can visualise the complete state space in a two-dimensional scatter plot. The data of both labels are organised along a ring. There is a certain amount of randomness added to create data distributed normally around the ring.

The tricky thing about such a data distribution is that in a standard view of the data, the histogram, the clear state space organisation is not visible. There are e.g. no two distinct mean values of the distributions. Also, while the two features are clearly dependent on each other (as seen in the scatter plot), it is not possible to regress one with the other by means of fits of the type y = f(x).

We will now use different classes of machine learning models to fit to these labelled data.

Classification Algorithms

Different classification algorithms approach problems differently. Let us name the algorithms in SciKit Learn.

SciKit Learn provides the following algorithms for classification problems:

• Ensemble: Averaging:
  • Random Forest
  • Extra Tree
  • Isolation Forest
  • Bagging
  • Voting
• Boosting:
  • Gradient Boosting
  • AdaBoost
• Decision Trees:
  • Decision Tree
  • Extra Tree
• Nearest Neighbour:
  • K Nearest Neighbour
  • Radius Neighbours
  • Nearest Centroid
• Support Vector Machine:
  • with non-linear kernel:
    • Radial Basis Function (RBF) Polynomial
    • Sigmoid
  • with linear kernel:
    • Linear kernel
  • parametrised with non-linear kernel:
    • Nu-Support Vector Classification
• Neural Networks:
  • Multi-layer Perceptron
  • Gaussian:
    • Gaussian Process
  • Linear Models:
    • Logistic Regression
    • Passive Aggressive
    • Ridge
    • Linear classifiers with Stochastic Gradient Descent
• Baysian:
  • Bernoulli
  • Multinomial
  • Complement

Some of these algorithms require a more in-depth understanding of how they work. To that end, we only review the performance of those that are easier to implement and adjust.

AdaBoost

The AdaBoost algorithm is special in that it does not work on its own; instead, it complements another ensemble algorithm (e.g. Random Forest) and boosts its performance by weighing the training data through a boosting algorithm. Note that boosting the performance does not necessarily translate into a better fit. This is because boosting algorithms are generally robust against over-fitting, meaning that they always try to produce generalisable models.

Seeding

Most machine learning algorithms rely on random number generation to produce results. Therefore, one simple, but important adjustment is to seed the number generator, and thereby making our comparisons more consistent; i.e. ensure that all models use the same set of random numbers. Almost all SciKit Learn models take an argument called random_state, which takes an integer number to seed the random number generator.

Training and Testing

Here is code to import a number of classifiers from SciKit Learn, fit them to the training data and predict the (complete) state space. The result is plotted below.

PYTHON

from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier

classifiers = {
    'Random Forest': RandomForestClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Random Forest)': AdaBoostClassifier(RandomForestClassifier(random_state=RANDOM_STATE)),
    'Extra Trees': ExtraTreesClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Extra Tree)': AdaBoostClassifier(ExtraTreesClassifier(random_state=RANDOM_STATE)),
    'Decision Tree': DecisionTreeClassifier(random_state=RANDOM_STATE),
    'SVC (RBF)': SVC(random_state=RANDOM_STATE),
    'SVC (Linear)': LinearSVC(random_state=RANDOM_STATE),
    'Multi-layer Perceptron': MLPClassifier(max_iter=5000, random_state=RANDOM_STATE)
}

PYTHON

ft_min, ft_max = -1.5, 1.5

# Constructing (2 grids x 300 rows x 300 cols):
grid_1, grid_2 = mgrid[ft_min:ft_max:.01, ft_min:ft_max:.01]

# We need only the shape for one of the grids (i.e. 300 x  300):
grid_shape = grid_1.shape

# state space grid for testing
new_obs = c_[grid_1.ravel(), grid_2.ravel()]

PYTHON

contour_levels = linspace(0, 1, 6)

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    clf.fit(X, y)
    y_pred = clf.predict(new_obs)
    y_pred_grid = y_pred.reshape(grid_shape)

    ax.scatter(X[:, feature_1], X[:, feature_2], c=y, s=1, cmap='bwr_r')
    ax.contourf(grid_1, grid_2, y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels)
    ax.set_ylim(ft_min, ft_max)
    ax.set_xlim(ft_min, ft_max)
    ax.set_yticks([-1.5, 0, 1.5])
    ax.set_xticks([-1.5, 0, 1.5])
    ax.set_title(name, fontsize=10);

show()

Seven of the eight classifiers were able to separate the inner data set from the outer data set successfully. The main difference is that some algorithms ended up with a more rectangular shape of the boundary whereas the others found a more circular form which reflects the original data distribution more closely. One classifier simply fails: the support vector classifier (SVC) with linear basis functions: it tries to fit a straight line to separate the classes which in this case is impossible.

The Train-Test Split

We will now modify our workflow to avoid the need to create separate testing data (the typical situation when dealing with recorded data). For this we start with a data set of n labelled samples. Of these n samples, a certain percentage is used for training (using the provided labels) and the rest for testing (withholding the labels). The testing data then do not need to be prepared separately.

The function we use is train_test_split from SciKit Learn. A nice feature of this function is that it tries to preserve the ratio of labels in the split. E.g. if the data contain 70% of True and 30 % of False labels, the algorithm tries to preserve this ratio in the split as good as possible: around 70% of the training data and of the testing data will have the True label.

PYTHON

from sklearn.model_selection import train_test_split

X, y = make_circles(n_samples=1000, factor=0.3, noise=.05, random_state=RANDOM_STATE)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=RANDOM_STATE, shuffle=True)

print(X_train.shape, X_test.shape)

OUTPUT

(700, 2) (300, 2)

Here is an illustration of the two sets of data. The splitting into testing and training data is done randomly. Picking test data randomly is particularly important for real data as it helps to reduce potential bias in the recording order.

PYTHON

fig, ax = subplots(figsize=(7, 6), ncols=2, nrows=2, sharex=True)

ax[0, 0].scatter(X_train[:, feature_1], X_train[:, feature_2], c=y_train, s=4, cmap='bwr')
ax[0, 1].scatter(X_test[:, feature_1], X_test[:, feature_2], c=y_test, s=4, cmap='bwr')

ax[1, 0].hist(X_train)
ax[1, 1].hist(X_test)

ax[0, 0].set_title('Training data')
ax[0, 1].set_title('Test data')

ax[0, 0].set_ylim(ft_min, ft_max)
ax[0, 1].set_ylim(ft_min, ft_max)

ax[1, 0].set_ylim(0, 100)
ax[1, 1].set_ylim(0, 100);

show()

Now we can repeat the training with this split dataset using eight types of models as above.

To compare the model performances, we use scoring: the method .score takes as input arguments the testing samples and their true labels. It then uses the model predictions to calculate the fraction of labels in the testing data that were predicted correctly.

There are different techniques to evaluate the performance, but the .score method provides a quick, simple, and handy way to assess a model. As far as classification algorithms in SciKit Learn are concerned, the method usually produces the mean accuracy, which is between 0 and 1; and the higher the score, the better the fit.

PYTHON

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    # Training the model using training data:
    clf.fit(X_train, y_train)

    y_pred = clf.predict(new_obs)
    y_pred_grid = y_pred.reshape(grid_shape)

    # Evaluating the score using test data:
    score = clf.score(X_test, y_test)

    # Scattering the test data only:
    ax.scatter(X_test[:, feature_1], X_test[:, feature_2], c=y_test, s=4, cmap='bwr', marker='.')

    ax.contourf(grid_1, grid_2, y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels)
#    ax.contourf(grid[0], grid[1], y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels)

    ax.set_ylim(ft_min, ft_max)
    ax.set_xlim(ft_min, ft_max)
    ax.set_yticks([-1.5, 0, 1.5])
    ax.set_xticks([-1.5, 0, 1.5])

    label = '{} - Score: {:.2f}'.format(name, score)
    ax.set_title(label , fontsize=10);

show()

Here, we only plotted the test data, those that were classified based on the trained model. The gray area shows the result of the classification: within the gray area the prediction is 1 (the red samples) and outside it is 0 (the blue samples). The result is that testing data are classified correctly in all but one of the classifiers, so their performance is 1, or 100 %. This is excellent because it demonstrates that most classifiers are able to deal with embedded topologies.

Let us now repeat the procedure with a higher level of noise to make the task more complicated.

PYTHON

X, y = make_circles(n_samples=1000, factor=.5, noise=.3, random_state=RANDOM_STATE)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=RANDOM_STATE, shuffle=True)

fig, ax = subplots(figsize=(7, 6), ncols=2, nrows=2, sharex=True)

ax[0, 0].scatter(X_train[:, feature_1], X_train[:, feature_2], c=y_train, s=4, cmap='bwr')
ax[0, 1].scatter(X_test[:, feature_1], X_test[:, feature_2], c=y_test, s=4, cmap='bwr')


ax[1, 0].hist(X_train)

ax[1, 1].hist(X_test)

ax[0, 0].set_title('Training data')
ax[0, 1].set_title('Test data')

ax[0, 0].set_ylim(-3, 3)
ax[0, 1].set_ylim(-3, 3)

ax[1, 0].set_ylim(0, 200)
ax[1, 1].set_ylim(0, 200);

show()

PYTHON

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    # Training the model using training data:
    clf.fit(X_train, y_train)

    y_pred = clf.predict(new_obs)
    y_pred_grid = y_pred.reshape(grid_shape)

    # Evaluating the score using test data:
    score = clf.score(X_test, y_test)

    # Scattering the test data only:
    ax.scatter(X_test[:, feature_1], X_test[:, feature_2], c=y_test, s=4, cmap='bwr', marker='.')

    ax.contourf(grid_1, grid_2, y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels)

    ax.set_ylim(ft_min, ft_max)
    ax.set_xlim(ft_min, ft_max)
    ax.set_yticks([-1.5, 0, 1.5])
    ax.set_xticks([-1.5, 0, 1.5])

    label = '{} - Score: {:.2f}'.format(name, score)
    ax.set_title(label , fontsize=10);

show()

Now the data are mixed in the plane and there is no simple way to separate the two classes. We can see in the plots how the algorithms try to cope with their different strategies. One thing that is immediately obvious is that the fitting patterns are different. Particularly, we can see the fragmented outcome of the decision tree classifier and the smooth elliptic area found by the support vector classifier (SVC) with radial basis functions (RBF) and the neural network (MLP). On a closer look, you may also notice that with ensemble methods in the upper row, the patterns are somewhat disorganised. This is due to the way ensemble methods work: they sample the data randomly and then class them into different categories based on their labels.

If the prediction was made by chance (throwing a dice), one would expect a 50 % score. Thus, the example also shows that the performance depends on the type of problem and that this testing helps to find an optimal classifier.

Never expose the test data

Testing a model on data that is used in training is a methodological mistake. It is therefore vital that the test data is never, ever used for training a model at any stage. This is one of the most fundamental principles of machine learning, and its importance cannot be exaggerated. There are numerous examples of people making this mistake one way or another, especially where multiple classification algorithms are used to address a problem.

The Stratified Shuffle Split

---

One potential bias arises when we try to improve the performance of our models through the change of the so-called hyperparameters (instead of using the default parameters as we did so far). We will always receive the optimal output given the specific test data chosen. This may lead to overfitting the model on the chosen training and testing data. This can be avoided by choosing different splits into testing and training data and repeating the fit procedure. Doing different splits while preserving the fraction of labels of each class in the original data, the method is called the stratified shuffle split.

We first need to import and instantiate the splitter. We set key word argument n_splits to determine the number of different splits. test_size lets us determine what fraction of samples is used for the testing data.

PYTHON

from sklearn.model_selection import StratifiedShuffleSplit

sss = StratifiedShuffleSplit(random_state=RANDOM_STATE, n_splits=10, test_size=0.3)

Let us look at the different splits obtained:

PYTHON

fig, ax = subplots(figsize=[10, 5])

n_splits = sss.n_splits
split_data_indices = sss.split(X=X, y=y)

for index, (tr, tt) in enumerate(split_data_indices):
    indices = X[:, feature_1].copy()
    indices[tt] = 1
    indices[tr] = 0

    # Visualize the results
    x_axis = arange(indices.size)
    y_axis = [index + .5] * indices.size
    ax.scatter(x_axis, y_axis, c=indices, marker='_', lw=10, cmap='coolwarm', vmin=-.2, vmax=1.2)

# Plot the data classes and groups at the end
class_y = [index + 1.5] * indices.size
ax.scatter(x_axis, class_y, c=y, marker='_', lw=10, cmap='coolwarm')

# Formatting
ylabels = list(range(n_splits))
ylabels.extend(['Data'])

ax.set_yticks(arange(n_splits + 1) + .5)
ax.set_yticklabels(ylabels)
ax.set_xlabel('Sample index')
ax.set_ylabel('SSS iteration');

show()

By choosing n_splits=10, we obtained ten different splits that have similarly distributed train and test data subsets from the original data. The fraction of the data set aside for testing is 30 %. The different splits cover the whole data set evenly. As such, using them for training and testing will lead to a fairly unbiased average performance.

Let us look at the data in state space to check that the classification task is now a real challenge.

PYTHON

fig, ax = subplots(figsize=(8, 8))

for train_index, test_index in sss.split(X, y):
    ax.scatter(X[train_index, 0], X[train_index, 1], c=y[train_index], cmap='Set1', s=30, marker='^', alpha=.5)
    ax.scatter(X[test_index, 0], X[test_index, 1], c=y[test_index], cmap='cool', s=30, alpha=.5, marker='*', label='Test');

show()

These are the scatter plots of the training (magenta) and testing (blue) data. Here are their distributions:

PYTHON

fig, ax = subplots(figsize=(8, 8))

for train_index, test_index in sss.split(X, y):
    ax.hist(X[train_index], color=['magenta', 'red'], alpha=.5, histtype='step')
    ax.hist(X[test_index], color=['cyan', 'blue'], alpha=.4, histtype='step');

show()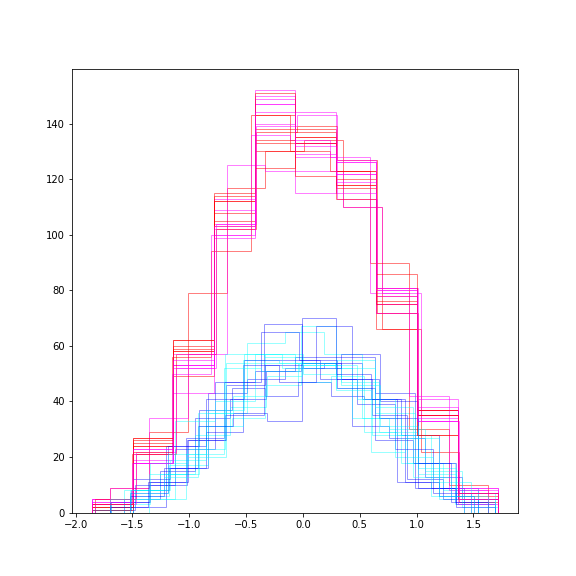

The distributions differ in height because less data are in the testing test. Otherwise they are similarly centred and spread. Using a number of realisations (instead of just one) we expect to obtain a more accurate and robust result of the training.

We now train our classifiers on these different splits and obtain the respective scores. They will give a robust measure of the classifier’s performance given the data and avoid potential bias due to the selection of specific test data.

PYTHON

X, y = make_circles(n_samples=1000, factor=.3, noise=.4, random_state=RANDOM_STATE)

split_data_indices = sss.split(X=X, y=y)

score = list()

for train_index, test_index in sss.split(X, y):
    X_s, y_s = X[train_index, :], y[train_index]
    new_obs_s, y_test_s = X[test_index, :], y[test_index]

    score_clf = list()

    for name, clf in classifiers.items():

        clf.fit(X_s, y_s)
        y_pred = clf.predict(new_obs_s)
        score_clf.append(clf.score(new_obs_s, y_test_s))

    score.append(score_clf)

score_mean = mean(score, axis=0)

bins = arange(len(score_mean))

fig, ax = subplots()

ax.bar(bins, score_mean);
ax.set_xticks(arange(0,8)+0.4)
ax.set_xticklabels(classifiers.keys(), rotation=-70);

show()

print(classifiers.keys())
print('Average scores: ')
print(["{0:0.2f}".format(ind) for ind in score_mean])

MLPClassifier(max_iter=5000, random_state=1234)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OUTPUT

dict_keys(['Random Forest', 'AdaBoost (Random Forest)', 'Extra Trees', 'AdaBoost (Extra Tree)', 'Decision Tree', 'SVC (RBF)', 'SVC (Linear)', 'Multi-layer Perceptron'])
Average scores:
['0.76', '0.76', '0.75', '0.75', '0.70', '0.79', '0.50', '0.78']

The result is the average score for the ten splits performed. All results for the noise-contaminated data are now in the seventies.

This is still good given the quality of the data. It appears that the decision tree classifier gives the lowest result for this kind of problem, SVC (RBF) scores highest. We have to keep in mind, however, that we are using the classifiers with their default settings. We will later use variation of the so-called hyperparameters to further improve the classification score.

Here we have used a for loop to train and test on each of the different splits of the data. SciKit Learn also contains functions that take the stratified shuffle split as an argument, e.g. permutation_test_score. In that case, the splits do not need to be done separately.

We have now reached a point where we can trust to have a robust and unbiased outcome of the training. Let us now look at more refined ways to quantify the result.

Evaluation: ROC and AUC

---

There are various measures that may be used to evaluate the performance of a machine learning model. Such measures look at different characteristics, including the goodness of fit and generalisability of a model. Evaluation measures used with regards to classification models include, but are not limited to:

• Receiver Operation Characteristic (ROC) and Area Under the Curve (AUC) - for binary classifiers.
• Accuracy
• Precision
• Recall

There are many other metrics that, depending on the problem, we may use to evaluate a machine learning model. Please see the official documentations for additional information on these measures and their implementation in SciKit Learn.

The quantities we are going to look at are the Receiver Operation Characteristic (ROC) and the Area Under the Curve (AUC).

A receiver operation characteristic, often referred to as the ROC curve, is a visualisation of the discrimination threshold in a binary classification model. It illustrates the rate of true positives (TPR) against the rate of false positives (FPR) at different thresholds. The aforementioned rates are essentially defined as:

• True Positive Rate (TPR): the sensitivity of the model
• False Positive Rate (FPR): one minus the specificity of the model

This makes ROC a measure of sensitivity versus specificity.

The area under the ROC curve, often referred to as AUC, reduces the information contained within a ROC curve down to a value between 0 and 1, with 1 being a perfect fit. An AUC value of 0.5 represents any random guess, and values below demonstrate a performance that’s even worse than a lucky guess!

Discussion

SciKit Learn includes specialist functions called roc_curve and roc_auc_score to obtain ROC (FPR and TPR values for visualisation) and AUC respectively. Both functions receive as input arguments the test labels (i.e. y_test) and the score (probability) associated with each prediction. We obtain the latter measure using one of the following two techniques:

• Decision function: where classification models have a .decision_function method that provides us with score associated with each label.
• Probability: where classification models have a .predict_proba method that provides us with the probability associated with each prediction (we used it in the Classification Introduction lesson). In this case, however, the results are provided in the form of a two-dimensional array where columns represent different labels (as defined in property). Given that we will plot ROC curves for binary problems (two labels), we only pick one of these columns. Usually, the second column (the feature representing True or 1) is the one to choose. However, if you notice that the results are unexpectedly bad, you may try the other column just be sure.

We can see that our classifiers now reach different degrees of prediction. The degree can be quantified by the Area Under the Curve (AUC). It refers to the area between the blue ROC curve and the orange diagonal. The area under the ROC curve, often referred to as AUC, reduces the information contained within a ROC curve down to a value between and 0 and 1, with 1 being a perfect fit. An AUC value of 0.5 represents a random guess, and values below the diagonal demonstrate a performance that’s even worse than a guess!

SciKit Learn includes specialist functions called roc_curve and roc_auc_score to obtain ROC (FPR and TPR values for visualisation) and AUC respectively. Both function receive as input arguments the test labels (i.e. y_score) and the score (probability) associated with each prediction. We obtain the latter measure using one of the following two techniques:

• Decision function: where classification models have a .decision_function method that provides us with a score associated with each label.
• Probability: where classification models have a predict_proba_ method that provides us with the probability associated with each prediction. In this case, however, the results are provided in the form of a two-dimensional array where columns represents different labels (as defined in .classes property). Given that we only plot ROC curves for binary problems, we should only use one of these columns. Usually, the second column (the feature representing True or 1) is the one to choose. However, if you notice that the results are unexpectedly bad, you may try the other column just be sure.

PYTHON

from sklearn.metrics import roc_curve, roc_auc_score

fig, all_axes = subplots(figsize=[15, 10], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    clf.fit(X_train, y_train)

    # Checking whether or not the object has `decision_function`:
    if hasattr(clf, 'decision_function'):
        # If it does:
        y_score = clf.decision_function(X_test)
    else:
        # Otherwise:
        y_score = clf.predict_proba(X_test)[:, feature_2]  # We only need one column.

    # Obtaining the x- and y-axis values for the ROC curve:
    fpr, tpr, thresh = roc_curve(y_test, y_score)

    # Obtaining the AUC value:
    roc_auc = roc_auc_score(y_test, y_score)

    ax.plot(fpr, tpr, lw=2)
    ax.plot([0, 1], [0, 1], lw=1, linestyle='--')

    ax.set_xlabel('False Positive Rate')
    ax.set_ylabel('True Positive Rate')

    label = '{} - AUC: {:.2f}'.format(name, roc_auc)
    ax.set_title(label, fontsize=10)

show()

The (orange) diagonal represents predictions of the two labels by a coin toss. To be of value the classifier must reach a ROC curve above the diagonal.

This concludes our first steps into classification with SciKit Learn. There are many more aspects of classification. From a practical point of view, data normalisation and permutation test score as well as the workflow report are important. These will be the topics of our next lesson.

Exercises

---

End of chapter Exercises

Take the torus-within-a-torus data generator from the Challenge above.

1. Create data with three features and a noise level of 0.3.

2. Create a pseudo-3D scatter plot of one of the test data sets to judge the difficulty of the task.

3. Train the above introduced classifiers using the stratified shuffle split to generate 10 sets of testing and training data and obtain the average score for each classifier.

4. Plot the feature importances obtained from the Random Forest classifier to see the contributions of each feature to the outcome.

Note that with 3 or more features it is no longer possible to see the full state space in a plane.

5. Optional: Check how the outcome varies depending on

   • Choice of seed for random number generator
   • Number of data splits
   • Percentage of data withheld for testing

Recommendation

Pick any of the provided (or other) data sets with labels to repeat the above. Feel free to try and do any testing or plotting that you find important. This is not an assignment to get the correct answer. Rather at this stage, we practise to use functionality from SciKit-learn to search for structure in the data that helps to achieve the best predictions possible.

Please check these solutions only after submitting the assignments.

PYTHON

from numpy import mgrid, linspace, arange, mean, array
from numpy.random import uniform, seed

from matplotlib.ticker import LinearLocator, FormatStrFormatter
from mpl_toolkits import mplot3d
from matplotlib.pyplot import subplots, axes, scatter, xticks, show

PYTHON

def make_torus_3D(n_samples=100, shuffle=True, noise=None, random_state=None,
                 factor=.8):
    """Make a large torus containing a smaller torus in 3d.

    A toy dataset to visualize clustering and classification
    algorithms.

    Read more in the :ref:`User Guide <sample_generators>`.

    Parameters
    ----------
    n_samples : int, optional (default=100)
        The total number of points generated. If odd, the inner circle will
        have one point more than the outer circle.

    shuffle : bool, optional (default=True)
        Whether to shuffle the samples.

    noise : double or None (default=None)
        Standard deviation of Gaussian noise added to the data.

    random_state : int, RandomState instance or None (default)
        Determines random number generation for dataset shuffling and noise.
        Pass an int for reproducible output across multiple function calls.
        See :term:`Glossary <random_state>`.

    factor : 0 < double < 1 (default=.8)
        Scale factor between inner and outer circle.

    Returns
    -------
    X : array of shape [n_samples, 2]
        The generated samples.

    y : array of shape [n_samples]
        The integer labels (0 or 1) for class membership of each sample.
    """
    from numpy import pi, linspace, cos, sin, append, ones, zeros, hstack, vstack, intp
    from sklearn.utils import check_random_state, shuffle

    if factor >= 1 or factor < 0:
        raise ValueError("'factor' has to be between 0 and 1.")

    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out

    co, ao, ci, ai = 3, 1, 3.6, 0.2
    generator = check_random_state(random_state)
    # to not have the first point = last point, we set endpoint=False
    linspace_out = linspace(0, 2 * pi, n_samples_out, endpoint=False)
    linspace_in  = linspace(0, 2 * pi, n_samples_in,  endpoint=False)
    outer_circ_x = (co+ao*cos(linspace_out)) * cos(linspace_out*61.1)
    outer_circ_y = (co+ao*cos(linspace_out)) * sin(linspace_out*61.1)
    outer_circ_z =    ao*sin(linspace_out)

    inner_circ_x = (ci+ai*cos(linspace_in)) * cos(linspace_in*61.1)* factor
    inner_circ_y = (ci+ai*cos(linspace_in)) * sin(linspace_in*61.1) * factor
    inner_circ_z =    ai*sin(linspace_in) * factor

    X = vstack([append(outer_circ_x, inner_circ_x),
                append(outer_circ_y, inner_circ_y),
                append(outer_circ_z, inner_circ_z)]).T

    y = hstack([zeros(n_samples_out, dtype=intp),
                   ones(n_samples_in, dtype=intp)])

    if shuffle:
        X, y = shuffle(X, y, random_state=generator)

    if noise is not None:
        X += generator.normal(scale=noise, size=X.shape)

    return X, y

PYTHON

from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.metrics import roc_curve, roc_auc_score

RANDOM_STATE = 123


classifiers = {
    'Random Forest': RandomForestClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Random Forest)': AdaBoostClassifier(RandomForestClassifier(random_state=RANDOM_STATE)),
    'Extra Trees': ExtraTreesClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Extra Tree)': AdaBoostClassifier(ExtraTreesClassifier(random_state=RANDOM_STATE)),
    'Decision Tree': DecisionTreeClassifier(random_state=RANDOM_STATE),
    'SVC (RBF)': SVC(random_state=RANDOM_STATE),
    'SVC (Linear)': LinearSVC(random_state=RANDOM_STATE),
    'Multi-layer Perceptron': MLPClassifier(max_iter=5000, random_state=RANDOM_STATE)
}

Q1 and Q2

PYTHON

seed(RANDOM_STATE)

X, y = make_torus_3D(n_samples=2000, factor=.5, noise=.3, random_state=RANDOM_STATE)

feature_1, feature_2, feature_3 = 0, 1, 2

fig, ax = subplots(figsize=(12, 9))
ax.set_visible(False)

ax = axes(projection="3d")

im = ax.scatter3D(X[:, feature_1], X[:, feature_2], X[:, feature_3],
                  marker='o', s=20, c=y, cmap='bwr');

ax.set_xlabel('Feature A')
ax.set_ylabel('Feature B')
ax.set_zlabel('Feature C')

ax.view_init(30, 50);

show()

Q3

PYTHON

sss = StratifiedShuffleSplit(random_state=RANDOM_STATE, n_splits=10, test_size=0.3)

split_data_indices = sss.split(X=X, y=y)

score = list()

for train_index, test_index in sss.split(X, y):
    X_s, y_s = X[train_index, :], y[train_index]
    new_obs_s, y_test_s = X[test_index, :], y[test_index]

    score_clf = list()

    for name, clf in classifiers.items():

        clf.fit(X_s, y_s)
        y_pred = clf.predict(new_obs_s)
        score_clf.append(clf.score(new_obs_s, y_test_s))

    score.append(score_clf)

score_mean = mean(score, axis=0)

bins = arange(len(score_mean))

fig, ax = subplots()

ax.bar(bins, score_mean);

show()

print(classifiers.keys())
print('Average scores: ')
print(["{0:0.2f}".format(ind) for ind in score_mean])

MLPClassifier(max_iter=5000, random_state=123)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OUTPUT

dict_keys(['Random Forest', 'AdaBoost (Random Forest)', 'Extra Trees', 'AdaBoost (Extra Tree)', 'Decision Tree', 'SVC (RBF)', 'SVC (Linear)', 'Multi-layer Perceptron'])
Average scores:
['0.87', '0.88', '0.87', '0.87', '0.83', '0.89', '0.49', '0.88']

PYTHON

clf_RF = RandomForestClassifier(random_state=RANDOM_STATE)

clf_RF.fit(X_s, y_s)

y_pred = clf_RF.predict(new_obs_s)

score_RF = clf_RF.score(new_obs_s, y_test_s)

print('Random Forest score:', score_RF)

RandomForestClassifier(random_state=123)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OUTPUT

Random Forest score: 0.88

Q4

PYTHON

importances = clf_RF.feature_importances_

template = 'Feature 1: {:.1f}%; Feature 2: {:.1f}%; Feature 3: {:.1f}%'

print(template.format(importances[0]*100, importances[1]*100, importances[2]*100))

bins = arange(importances.shape[0])

fig, ax = subplots()

ax.bar(bins, importances, color=('g', 'm', 'b'));
ax.set_ylabel('Feature Importance', fontsize=16)

xticks(bins, ('Feature 1', 'Feature 2', 'Feature 3'), fontsize=16);

show()

OUTPUT

Feature 1: 31.4%; Feature 2: 33.9%; Feature 3: 34.7%

The three features contribute similarly to the outcome.

Key Points

• Different classification algorithms approach problems differently.
• train_test_split function tries to preserve the ratio of labels in the split
• Increasing the level of noise in the data makes the task more complicated.
• The potential bias due to splitting could be avoid using stratified shuffle split.
• StratifiedShuffleSplit is a method that uses n_splits and test_size parameters.

Content from Refinement

---

Last updated on 2024-08-06 | Edit this page

Download Chapter PDF

Download Chapter notebook (ipynb)

Mandatory Lesson Feedback Survey

Overview

Questions

• How do different evaluation metrics differ?
• What techniques are used to improve on chance prediction?
• What are the limitations of a confusion matrix?
• How can normalisation and hyperparameter tuning help to improve the results?
• How could test data leakage be avoided?

Objectives

• Introducing different types of metrics for model evaluation.
• Understanding the permutation score.
• Illustrating model evaluation using the confusion matrix.
• working with normalisation and hyperparameter tuning.
• The concept of progressive adjustment.

Import functions

PYTHON

from numpy import mgrid, linspace, c_, arange, mean, array
from numpy.random import uniform, seed
from sklearn.datasets import make_circles
from mpl_toolkits import mplot3d
from matplotlib.pyplot import subplots, axes, scatter, xticks, show

from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier

RANDOM_STATE = 111

classifiers = {
    'Random Forest': RandomForestClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Random Forest)': AdaBoostClassifier(RandomForestClassifier(random_state=RANDOM_STATE)),
    'Extra Trees': ExtraTreesClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Extra Tree)': AdaBoostClassifier(ExtraTreesClassifier(random_state=RANDOM_STATE)),
    'Decision Tree': DecisionTreeClassifier(random_state=RANDOM_STATE),
    'SVC (RBF)': SVC(random_state=RANDOM_STATE),
    'SVC (Linear)': LinearSVC(random_state=RANDOM_STATE),
    'Multi-layer Perceptron': MLPClassifier(max_iter=5000, random_state=RANDOM_STATE)
}

Revision Example with Circular Test Data

---

For our classification problem, we will use the make_circles function. See the documentation

The parameters for noise level and relative size of the two circles are such that the task becomes difficult.

PYTHON

seed(RANDOM_STATE)

X, y = make_circles(n_samples=500, factor=0.5, noise=.3, random_state=RANDOM_STATE)

feature_1, feature_2 = 0, 1
ft_min, ft_max = X.min(), X.max()

print('Shape of X:', X.shape)

fig, ax = subplots(figsize=(10, 5), nrows=1, ncols=2)

ax[0].scatter(X[:, feature_1], X[:, feature_2], c=y, s=4, cmap='bwr');
ax[0].set_xlabel('Feature 1')
ax[0].set_ylabel('Feature 1')
ax[1].hist(X);
ax[1].set_xlabel('Value')
ax[1].set_ylabel('Count')

show()

OUTPUT

Shape of X: (500, 2)

For training, we use the same classifiers as in the previous Lesson. We train on the whole data set and then use a meshgrid of the state space for prediction.

PYTHON

ft_min, ft_max = -1.5, 1.5

# Constructing (2 grids x 300 rows x 300 cols):
grid_1, grid_2 = mgrid[ft_min:ft_max:.01, ft_min:ft_max:.01]

# We need only the shape for one of the grids (i.e. 300 x  300):
grid_shape = grid_1.shape

# state space grid for testing
new_obs = c_[grid_1.ravel(), grid_2.ravel()]

PYTHON

contour_levels = linspace(0, 1, 6)

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):

    clf.fit(X, y)

    y_pred = clf.predict(new_obs)
    y_pred_grid = y_pred.reshape(grid_shape)
    print("")

    ax.scatter(X[:, feature_1], X[:, feature_2], c=y, s=1, cmap='bwr_r')
    ax.contourf(grid_1, grid_2, y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels);

    ax.set_ylim(ft_min, ft_max)
    ax.set_xlim(ft_min, ft_max)
    ax.set_yticks([ft_min, 0, ft_max])
    ax.set_xticks([ft_min, 0, ft_max])
    ax.set_title(name, fontsize=10);

show()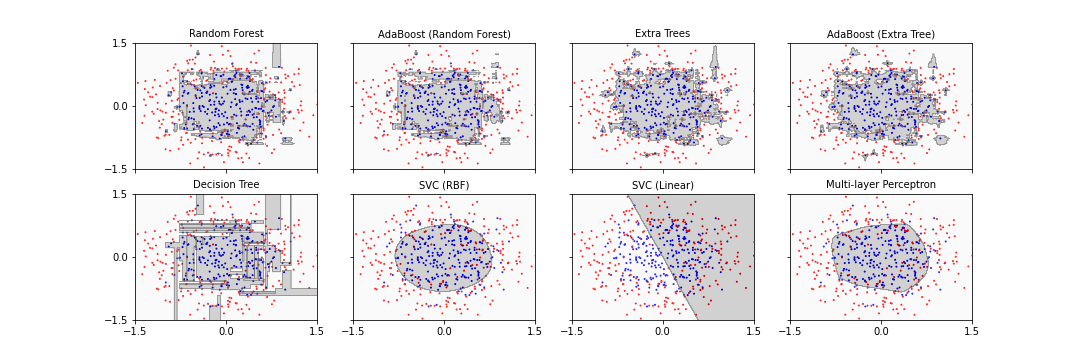

Seven of the eight classifiers are able to separate the inner data set from the outer data set successfully. The main difference is that some algorithms ended up with a more rectangular shape of the boundary whereas the others find a more circular form which reflects the original data distribution more closely. One classifier simply fails: SVC (linear). It tries to fit a straight line to separate the classes which in this case is impossible.

Note

Code: Note how the keyword argument sharey is used in the call of subplots to have y-axis only labelled once. The name of the classifier is extracted from the dictionary as its key and used to set up the title of each panel.

Metrics

---

We already used the score to evaluate the model performance. Here are some further metrics used in machine learning.

Accuracy is a metric that evaluates the integrity of the model by comparing true labels with their predicted counterparts. It produces a value between 0 and 1, where 1 is the best possible outcome, and \(1 / n_{classes}\) represents the probability of a random guess. See the Scikit-learn documentation for the accuracy_score. The mathematical formula can be found in the metrics and scoring section of the documentation.

Recall is a metric that evaluates the ability of a classification model to find true positive labels. The measure produces a scalar value between 0 and 1, where 1 is the perfect outcome. See the Scikit-learn documentation for the recall_score. The recall is the percentage of true predictions of the overall number of predictions. It is also known as sensitivity.

Average Precision, also referred to as AP, is a metric that produces a scalar value for the precision-recall curve between and with being the outcome. The metric obtains this value by weighing:

• the mean of precisions (P) at each threshold (n),
• the increase in recall (R) from the previous threshold (n-1).

The metric is mathematically defined as follows:

\[ AP = \sum_{n}^{}(R_n - R_{n-1}) \cdot P \]

Average precision vs AUC

As you may have noticed, the AUC metric also evaluates the area under the precision-recall curve using the trapezoid rule and with linear interpolation. The interpolation, however, may cause the resulting output to be better than it actually is. In other words, the AUC measure evaluates the outcome rather optimistically.

Precision is also called the positive predictive value.

F1 Score Another useful metric to evaluate a classification model that relies on precision and recall is the F1 Score, see the Scikit-learn documentation. It is mathematically defined as:

\[ F_1 = 2 \cdot \frac{P\cdot R}{P+R} \]

where \(P\) and \(R\) represent precision and recall, respectively.

Wikipedia has a nice summary of the measures and connections between them.

In Scikit-learn, these measures can be used in a standardised fashion. Here is an example using the recall_score.

PYTHON

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5, random_state=RANDOM_STATE, shuffle=True)

print(X_train.shape, X_test.shape)

OUTPUT

(250, 2) (250, 2)

PYTHON

from sklearn.metrics import recall_score

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):

    # Training the model using training data:
    clf.fit(X_train, y_train)

    y_pred_gr = clf.predict(new_obs)
    y_pred_grid = y_pred_gr.reshape(grid_shape)

    y_predicted = clf.predict(X_test)
    print("")
    # Evaluating the score using test data:
    score = clf.score(X_test, y_test)
    recall = recall_score(y_test, y_predicted)

    # Scattering the test data only:
    ax.scatter(X_test[:, feature_1], X_test[:, feature_2], c=y_test, s=4, cmap='bwr', marker='.')
    print("")
    ax.contourf(grid_1, grid_2, y_pred_grid, cmap='gray_r', alpha=.2, levels=contour_levels)

    ax.set_ylim(ft_min, ft_max)
    ax.set_xlim(ft_min, ft_max)
    ax.set_yticks([-1.5, 0, 1.5])
    ax.set_xticks([-1.5, 0, 1.5])

    label = '{} - Recall: {:.2f}'.format(name, recall)
    ax.set_title(label , fontsize=10);

show()

Reducing Bias on Test Data

Whilst SciKit Learn provides us with a dedicated function to obtain accuracy, the value it provides depends on how our training and test data have been split. Using the train-test-split, we can randomly shuffle the data to address this very problem. However, this implicitly assumed that our original data followed a specific distribution which is best represented by shuffling the data. That may not always be the case. In practice, we can never fully eliminate this type of bias. What we can do, however, is to split, shuffle, and permute the samples in the original dataset repeatedly to minimise the likelihood of bias.

Permutation Score

---

When dealing with biological and medical data, the results of machine learning often are not clear-cut. The question remains whether or not to trust a predictor as being truly above chance levels. An effective technique to address this is to randomly shuffle the labels independently of the data. I.e. we permutate only the labels, and check whether the classification score actually decreases. The permutation score then quantifies how trustworthy the result with the correct labels is. See the Scikit-learn documentation for details.

Now that we know about evaluation metrics, we are set to properly begin the evaluation process. We can use so-called cross-validators for testing the models if a test is run many times on data with differently permuted labels. To facilitate this, Scikit-learn provides the function permutation_test_score.

Note

The process of cross-validation is computationally expensive, as is the process of repeatedly permuting, fitting, and testing our models. In this context, we will be using both processes to complement each other. This makes the operation time-consuming and slow.

When possible, Scikit-learn provides us the with ability to use multiple CPU cores to speed up intensive computations through multiprocessing. Where available, this can be achieved by setting the n_jobs argument of a function or a class to the number of CPU cores we wish to use. Conveniently, it can be set to n_jobs=-1 to use all available CPU cores (see e.g. the Hyperparameter Tuning section below). Here, we have shown the use of only one core with n_jobs=1 which is computationally slow. You can adjust it according to the machine you are using to make it faster.

The keyword argument n_permutations is set to 100 by default. You can speed the cross-validation up by choosing a smaller number.

PYTHON

from sklearn.model_selection import permutation_test_score

n_classes = 2

chance = 1 / n_classes

fig, axes = subplots(figsize=[16, 12], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    score, permutation_scores, pvalue = permutation_test_score(clf, X, y, scoring="accuracy", n_jobs=1,n_permutations=100)

    score_label = 'Score: {:.3f}, (p={:.4f})'.format(score, pvalue)
    print("")
    chance_label = 'Chance: {:.3f}'.format(chance)

    ax.hist(permutation_scores)
    ax.axvline(score,  c='g', label=score_label,  linewidth=3.0)
    ax.axvline(chance, c='r', label=chance_label, linewidth=3.0)
    ax.set_title(name, fontsize=10)
    ax.legend(fontsize=8)

show()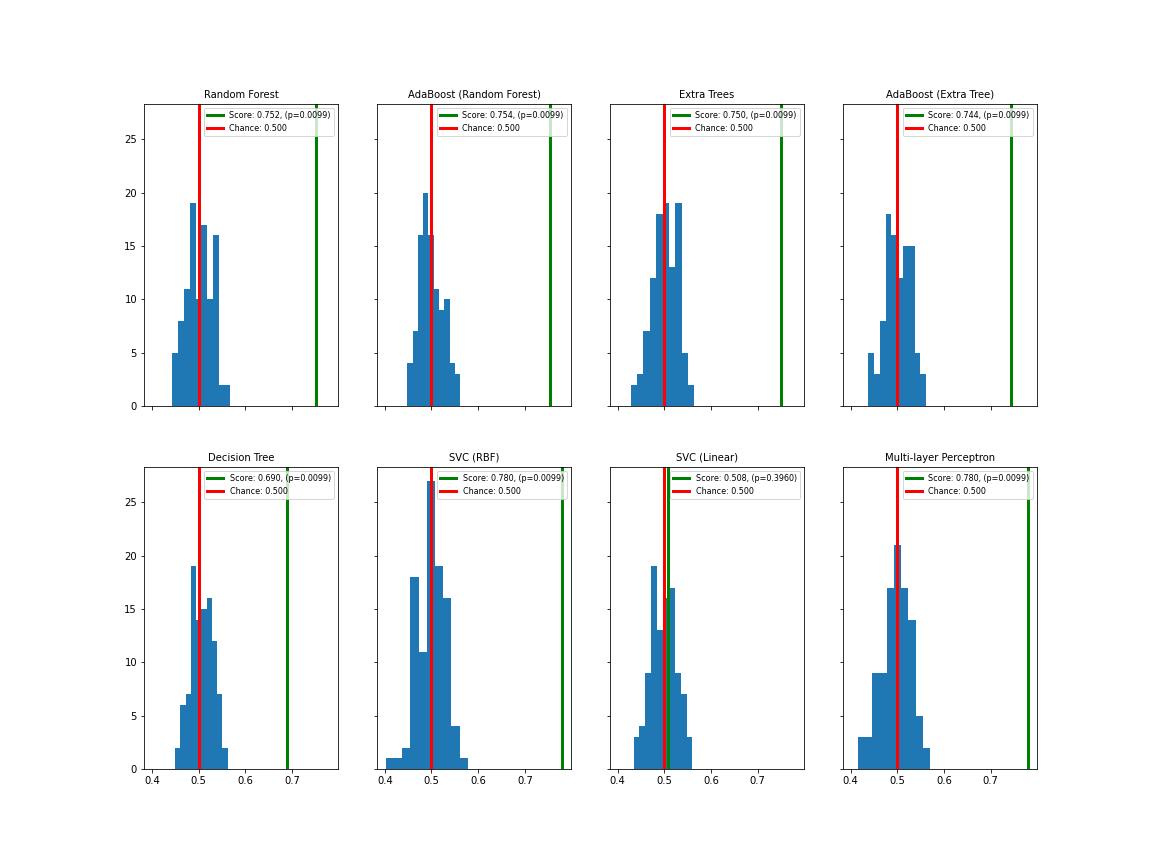

Apart from SVC (linear), all classifiers show satisfactory separation of the permutation test (blue distribution with red mean value) from the data score (green line). Apart from SVC (linear), the p-values are below 0.01.

Here is a Scikit-learn example using permutations with the Iris data.

Confusion Matrix

---

Another useful method to evaluate a model and demonstrate its integrity is to produce a confusion matrix. The matrix demonstrates the number of correctly predicted labels against the incorrect ones. As such it can, however, only be used for classification problems with two labels.

Scikit-learn provides a function to create a confusion matrix. Here is an expanded function to simplify the visualisation of this matrix.

PYTHON

def plot_confusion_matrix(y_test, y_pred, classes, normalize=False, ax=None):
    """
    This function prints and plots the confusion matrix.
    y_test (array)
    y_pred (array)
    classes (array)
    normalize (bool) Normalize the results (True), or show them as integer numbers (False).
    ax Visualization axis.
    The function is an adaptation of a SciKit Learn example.
    """

    from itertools import product
    from numpy import asarray, newaxis
    from sklearn.metrics import confusion_matrix
    cm = confusion_matrix(y_test,y_pred)
    n_classes = len(classes)

    if normalize:
        cm = asarray(cm).astype('float32') /cm.sum(axis=1)[:, newaxis]

    if not ax:
        from matplotlib.pyplot import subplots, show
        fig, ax = subplots()

    ticks = range(n_classes)
    ax.imshow(cm, interpolation='nearest', cmap='Blues')
    ax.set_xticks(ticks)
    ax.set_xticklabels(classes, rotation=90)
    ax.set_yticks(ticks)
    ax.set_yticklabels(classes)
    fmt = '.2f' if normalize else 'd'
    thresh = 3*cm.max() / 4
    cm_dim = cm.shape

    # Matrix indices:
    indices_a = range(cm_dim[0])
    indices_b = range(cm_dim[1])
    # Cartesian product of matrix indices:
    indices = product(indices_a, indices_b)
    fmt = '.2f' if normalize else 'd'

    for ind_a, ind_b in indices:
      label = format(cm[ind_a, ind_b], fmt)
      color = "white" if cm[ind_a, ind_b] > thresh else "black"
      ax.text(ind_b, ind_a, label, ha="center", color=color)
    ax.set_ylabel('True label')
    ax.set_xlabel('Predicted label')

    return ax

PYTHON

class_names = ('False (0)', 'True (1)')

fig, axes = subplots(figsize=(17, 12), ncols=4, nrows=2, sharey=True, sharex=True)


for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    clf.fit(X_train, y_train)

    y_pred = clf.predict(X_test)

    plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True, ax=ax)

    ax.set_title(name, fontsize=10);


show()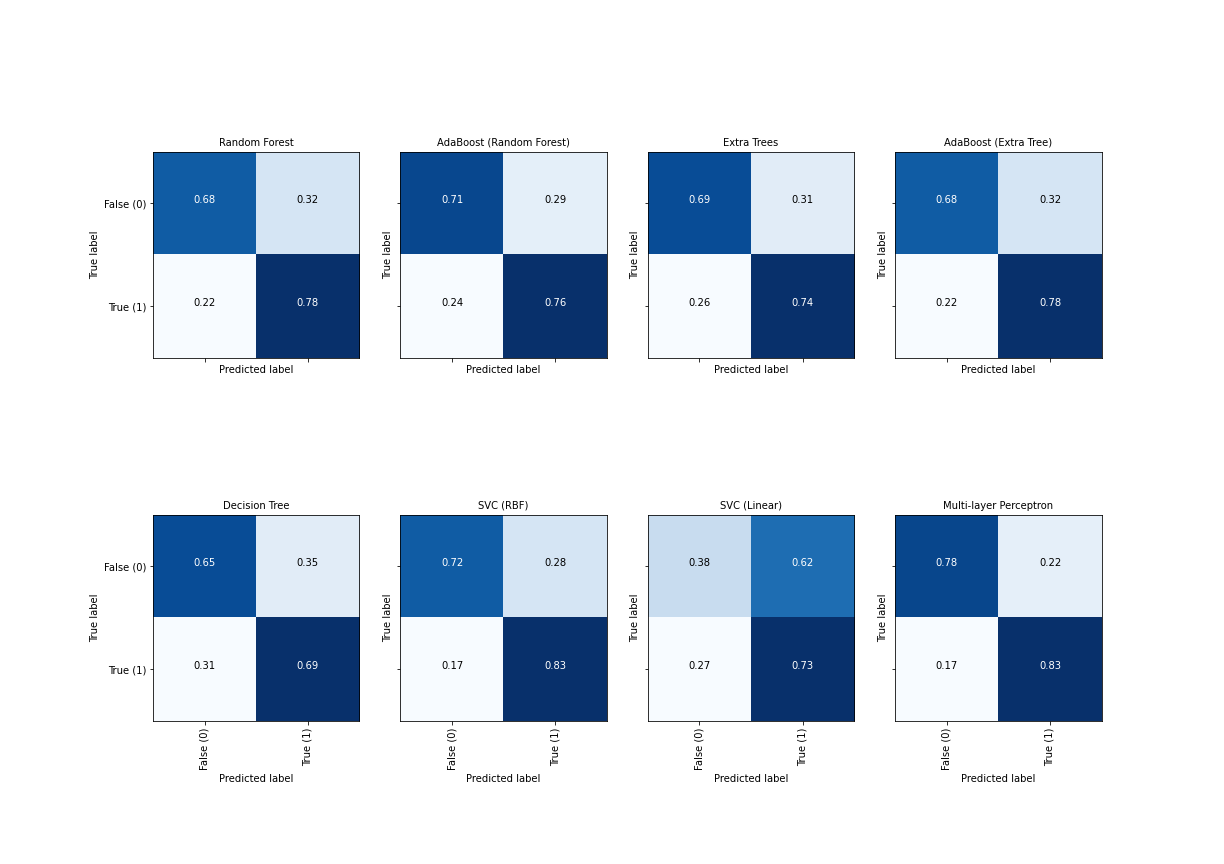

Ideally, the diagonal fields are both white and the off-diagonal fields maximally dark.

Further Refinements

---

Once we decide what algorithm to use, we start by training that algorithm with its default settings and evaluate the results. If not satisfied, we can make further adjustments to the hyper-parameters of the algorithm to improve the results. As always in machine learning, it is of great importance that we avoid overfitting, i.e. maintain the generalisability of the model whilst improving its performance.

We start by creating a classification problem with 3 features and 2 labels using the make_classification function. Data are now displayed in pseudo-3D.

PYTHON

from sklearn.datasets import make_classification

X, y = make_classification(
    n_samples=500,
    n_features=3,
    n_classes=2,
    n_informative=2,
    n_redundant=0,
    n_repeated=0,
    n_clusters_per_class=2,
    class_sep=.7,
    scale=3,
    random_state=RANDOM_STATE
)

fig, ax = subplots()

ax.hist(X);
ax.set_xlabel('Value')
ax.set_ylabel('Count')

show()

PYTHON

from mpl_toolkits.mplot3d import Axes3D

fig, ax = subplots(figsize=(10, 8), subplot_kw=dict(projection='3d'))

ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, s=5, cmap='bwr');
show()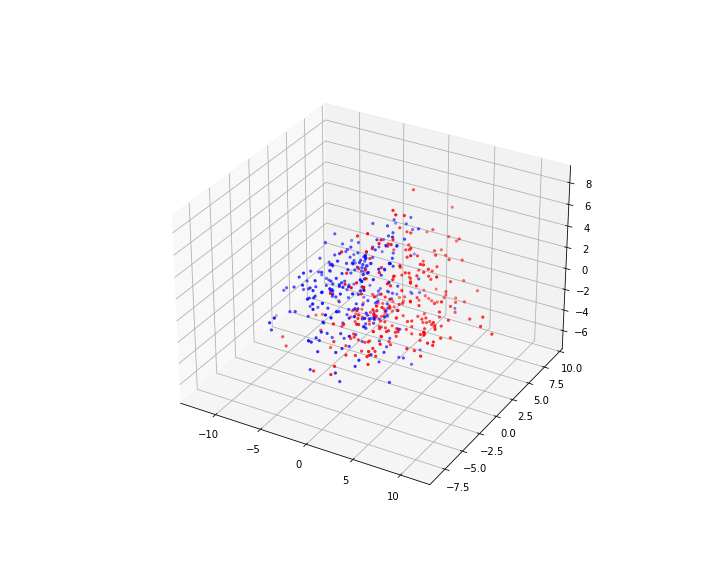

PYTHON

fig, axes = subplots(figsize=(12, 3), ncols=3, sharex=True, sharey=True)

axes[0].scatter(X[:, 0], X[:, 1], c=y, s=2, cmap='bwr')
axes[1].scatter(X[:, 0], X[:, 2], c=y, s=2, cmap='bwr')
axes[2].scatter(X[:, 1], X[:, 2], c=y, s=2, cmap='bwr');

show()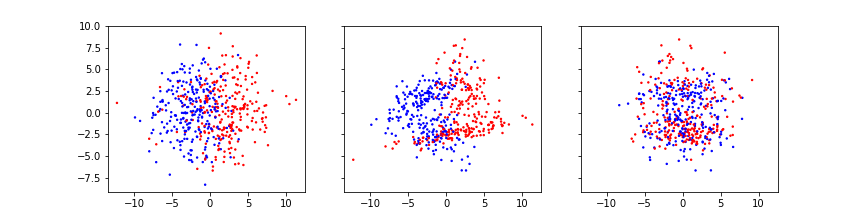

Note

Code: Note the setting up of 3D axis. Some examples with code to learn 3D plotting are provided in these tutorials.

We can now go ahead and use our classifier dictionary – which contains the classifiers with their default settings – to train and evaluate the models. We use the train-test split to evaluate the performance.

PYTHON

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.8, random_state=RANDOM_STATE, shuffle=True)

for name, clf in classifiers.items():
    clf.fit(X_train, y_train)
    score = clf.score(X_test, y_test)
    print('{:<30} Score: {:.2f}'.format(name, score))

MLPClassifier(max_iter=5000, random_state=111)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Normalisation

Depending on the nature of the data, it might be beneficial to normalise the data before fitting a classifier. This is widely done in machine learning but needs thought in each case.

Normalisation can be done in various ways. One common way to normalise data is to require that they have mean 0 and variance 1. This is used for example, when calculating the Pearson correlation coefficient. Another popular way in machine learning is to normalise data to Euclidean norm 1. For a data point in an m-dimensional feature space (m is the number of features), the Euclidean norm of a single point (one sample or row) is normalised such that the distance of the point from the origin is 1.

Let us first see an example: some data points are spread between 1 and 4.

PYTHON

from sklearn.preprocessing import Normalizer

some_data = array([[1, 4], [3, 1], [4, 4], [2, 3]])

norm_skl         = Normalizer()
some_data_normed = norm_skl.fit_transform(some_data)

print('Normalised data:', '\n', some_data_normed)

from numpy import amax

fig, ax = subplots(nrows=1, ncols=2)

scaling = amax(some_data)*1.1

ax[0].scatter(some_data[:, 0], some_data[:, 1])
ax[0].set_xlim(0, scaling)
ax[0].set_ylim(0, scaling)
ax[0].set_xlabel('Some data')

ax[1].scatter(some_data_normed[:, 0], some_data_normed[:, 1], c='r')
ax[1].set_xlim(0, scaling)
ax[1].set_ylim(0, scaling);
ax[1].set_xlabel('Normalised data')

show()

OUTPUT

Normalised data:
 [[0.24253563 0.9701425 ]
 [0.9486833  0.31622777]
 [0.70710678 0.70710678]
 [0.5547002  0.83205029]]
(0.0, 4.4)
(0.0, 4.4)
(0.0, 4.4)

Effectively, all normalised data are positioned on a circle around the origin with radius 1. Depending on correlations existing between the features this leads to different distortions of the original data.

Let us now apply this normalisation to our artificial data set.

PYTHON

norm = Normalizer()

X_normed = norm.fit_transform(X)

fig, ax = subplots(figsize=(8, 8), subplot_kw=dict(projection='3d'))

ax.scatter(X_normed[:, 0], X_normed[:, 1], X_normed[:, 2], c=y, s=5, cmap='bwr');
ax.view_init(30, 50);
show()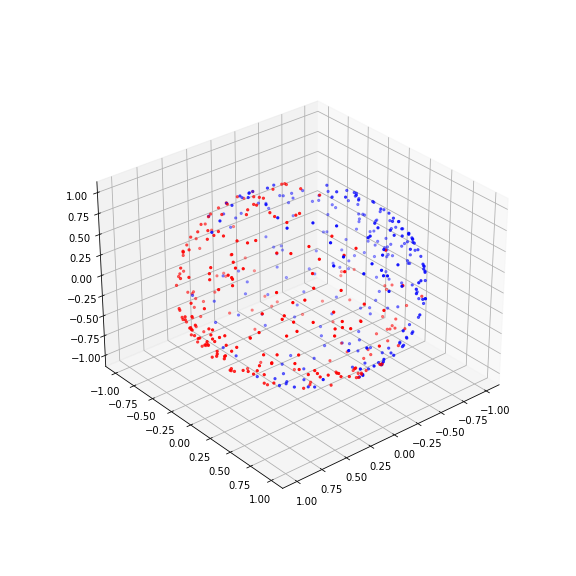

PYTHON

fig, axes = subplots(figsize=(10, 3), ncols=3, sharex=True, sharey=True)

axes[0].scatter(X_normed[:, 0], X_normed[:, 1], c=y, s=2, cmap='bwr')
axes[1].scatter(X_normed[:, 0], X_normed[:, 2], c=y, s=2, cmap='bwr')
axes[2].scatter(X_normed[:, 1], X_normed[:, 2], c=y, s=2, cmap='bwr');

show()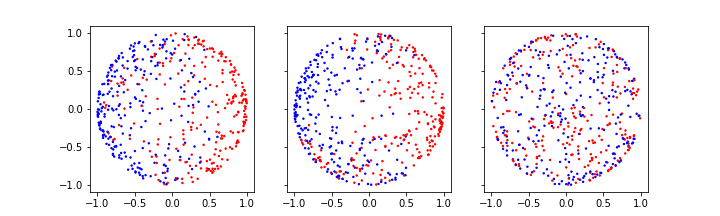

The normalisation projects the data on the unit sphere. And now we can do the training on the normalised data:

PYTHON

X_train, X_test, y_train, y_test = train_test_split(X_normed, y, test_size=.8, random_state=RANDOM_STATE, shuffle=True)

for name, clf in classifiers.items():
    clf.fit(X_train, y_train)
    score = clf.score(X_test, y_test)
    print('{:<30} Score: {:.2f}'.format(name, score))

MLPClassifier(max_iter=5000, random_state=111)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Due to the homogeneous nature of the artificial data, the results here are comparable for the data and their normalised version. But this may change when using data with inconsistent distributions of the columns. For an example, see the breastcancer data used in the assignment.

Hyperparameter Tuning

Once we decide on what algorithm to use, we often start by training that algorithm with its default settings and evaluate the results. If not satisfied, we can go further and make adjustments to the hyper-parameters of the algorithm to improve the results. As always in machine learning, it is of great importance that we maintain the generalisability of our model whilst improving its performance. We use the data from the above classification problem with 3 features and 2 labels.

Progressive Adjustment

After we have compared original and normalised data and obtained their scores, we now can try to progressively improve the performance of the algorithms. Each classification algorithm uses a unique set of hyper-parameters, the details of which are outlined in their respective documentations on Scikit-learn. The optimum parameters are those that produce the best fit whilst maintaining the generalisability of a model. One way to obtain the optimum settings is to test different parameters and compare the model scores over and over again. However, as outlined before, by doing so we may risk leaking our test data, and end up over-fitting the model to the test data. (We also learned above that we can use different cross-validators to address this problem.)

Scikit-learn provides us with a tool entitled GridSearchCV to define different values for different parameters. It then applies different combinations of different parameters to the model and evaluates the outcome using data that it generates from a cross-validation algorithm. Once finished, it provides us with the parameters that produce the best score for our data. This is referred to as progressive adjustment.

Note that this process can be lengthy, and may need to be refined several times, so it is a good idea to set n_jobs=-1 and thereby take advantage of different CPU core on the computer. For demonstration, we use SVC(rbf) as a classifier. With certain problems, its training may lead to poor results with the default parameters.

PYTHON

clf = SVC(kernel='rbf', C=1, gamma=100, tol=0.0001)

clf.fit(X_train, y_train)

score = clf.score(X_test, y_test)

print('{:<30} Score: {:.2f}'.format('SVC (RBF)', score))

SVC(C=1, gamma=100, tol=0.0001)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OUTPUT

SVC (RBF)                      Score: 0.68

Progressive adjustment of some of the parameters may lead to an improved model.

Check the documentation for the meaning and the default values of regularisation parameters C, kernel coeffcient gamma, and tolerance setting tol.

PYTHON

from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV

param_grid = dict(C=[1e-4, 1e-3, 1e-2, 1e-1, 1, 10],
                  gamma=[100, 1000, 10000, 100000],
                  tol=[1e-4, 1e-3, 1e-2, 1e-1])

cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=RANDOM_STATE)
clf = SVC(kernel='rbf', random_state=RANDOM_STATE)

grid = GridSearchCV(clf, param_grid=param_grid, cv=cv, n_jobs=1)

grid.fit(X, y)

print("ORIGINAL: Best parameters {}   Score: {:.2f}".format(grid.best_params_, grid.best_score_))

grid.fit(X_normed, y)

print("NORMED:   Best parameters {}    Score {:.2f}".format(grid.best_params_, grid.best_score_))

ORIGINAL: Best parameters {'C': 0.0001, 'gamma': 1000, 'tol': 0.0001}   Score: 0.65

NORMED:   Best parameters {'C': 1, 'gamma': 100, 'tol': 0.0001}    Score 0.75

In this case, while both optimised scores are better than the original one, there is also a notable improvement when using the normalised data. Let us similarly check the Random Forest classifier, first with default settings.

PYTHON

clf = RandomForestClassifier(random_state=RANDOM_STATE)

clf.fit(X_train, y_train)

score = clf.score(X_test, y_test)

print('{:<30} Score: {:.2f}'.format('Random Forest', score))

RandomForestClassifier(random_state=111)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OUTPUT

Random Forest                  Score: 0.77

And now a grid over some of its parameters.

PYTHON

from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV

param_grid = dict(
    n_estimators=[5, 10, 15, 20, 50, 60, 70],
    max_features=[None, 'auto', 'sqrt', 'log2'],
    min_samples_split=[2, 3, 4, 5],
    max_depth=[1, 2, 3, 4]
)

cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=RANDOM_STATE)

clf = RandomForestClassifier(random_state=RANDOM_STATE)

grid = GridSearchCV(clf, param_grid=param_grid, cv=cv, n_jobs=1)

grid.fit(X, y)

print("ORIGINAL: Best parameters {}   Score: {:.2f}".format(grid.best_params_, grid.best_score_))

grid.fit(X_normed, y)

print("NORMED:   Best parameters {}    Score {:.2f}".format(grid.best_params_, grid.best_score_))

ORIGINAL: Best parameters {'max_depth': 4, 'max_features': None, 'min_samples_split': 2, 'n_estimators': 15}   Score: 0.84

NORMED:   Best parameters {'max_depth': 3, 'max_features': 'auto', 'min_samples_split': 4, 'n_estimators': 10}    Score 0.81

In this case, our (arbitrary) search did not lead to a substantial improvement. This shows that the default settings are in fact a good starting point.

Leakage in progressive adjustments

We have already highlighted unequivocally the importance of not exposing our test data to our model during the training process; but where does training end? After deciding on an algorithm, we often attempt to improve its performance by adjusting its hyper-parameters as done above. We make these adjustments on our model repeatedly until we obtain optimal results in a specific metric that scores the performances based exclusively on our test data. In such cases, we risk leaking our test data and thereby over-fit our model to the test data through progressive adjustments. This means that the evaluation metrics on the generalisability of our model are no longer reliable.

One way to address this problem is to split our original data into 3 different datasets: training, test, and validation. Whilst this is a valid approach that may be used in specific circumstances, it might also introduce new problems, e.g. after splitting the available data into 3 subsets, there might just not be enough data to train the classifier properly.

See for example the discussion in part 2 of this paper on predictive modelling for brain stimulation. The above leaking is there referred to as “snooping”.

Exercises

---

End of chapter Exercises

As a suggestion, take the breast cancer dataset.

1. Using all features create a summary boxplot to see the medians and distributions of the features.

2. Train the above introduced classifiers using the train_test split to generate testing and training data and pick a small training set of e.g. 10% to make the classification task difficult. Obtain the recall scores to compare classifiers.

3. Plot the confusion matrix for each case.

4. Do a permutation test with default settings to get the p-values to reject the null hypothesis that the scores are compatible with random predictions. If it takes too long, reduce n_permutations.

5. Repeat the workflow with normalised data and compare the results.

6. Perform a hyperparameter tuning with the Random Forest classifier. For the optimal parameter settings, re-run the training and plot the feature importances to see the contributions of each feature to the outcome.

The breast cancer data can be imported from the scikit-learn.

PYTHON

from sklearn.datasets import load_breast_cancer

data = load_breast_cancer()

X = data.data
y = data.target

Feel free to try and do any other testing or plotting that you find important. This assignment is not meant to get a correct answer. It should help you to increase flexibility when facing a complex machine learning problem.

Please check these solutions only after submitting the assignments.

PYTHON

from numpy import mgrid, linspace, c_, arange, mean, array
from numpy.random import uniform, seed
from matplotlib.ticker import LinearLocator, FormatStrFormatter
from mpl_toolkits import mplot3d
from matplotlib.pyplot import subplots, axes, scatter, xticks

from sklearn.datasets import load_breast_cancer
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score

from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier

from sklearn.model_selection import permutation_test_score

from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV

RANDOM_STATE = 111

classifiers = {
    'Random Forest': RandomForestClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Random Forest)': AdaBoostClassifier(RandomForestClassifier(random_state=RANDOM_STATE)),
    'Extra Trees': ExtraTreesClassifier(random_state=RANDOM_STATE),
    'AdaBoost (Extra Tree)': AdaBoostClassifier(ExtraTreesClassifier(random_state=RANDOM_STATE)),
    'Decision Tree': DecisionTreeClassifier(random_state=RANDOM_STATE),
    'SVC (RBF)': SVC(random_state=RANDOM_STATE),
    'SVC (Linear)': LinearSVC(random_state=RANDOM_STATE, dual=False),
    'Multi-layer Perceptron': MLPClassifier(max_iter=5000, random_state=RANDOM_STATE)
    }

Notice that the linear Support Vector classifier is imported with the keyword argument dual=False. This is to reduce the number of (pink) warnings that occur when the classifier struggles to find a good solution.

Q1

PYTHON

data = load_breast_cancer()

X = data.data
y = data.target

print(X.shape, y.shape)

To get the feature names, you can access them as follows:

PYTHON

data.feature_names

OUTPUT

array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
       'mean smoothness', 'mean compactness', 'mean concavity',
       'mean concave points', 'mean symmetry', 'mean fractal dimension',
       'radius error', 'texture error', 'perimeter error', 'area error',
       'smoothness error', 'compactness error', 'concavity error',
       'concave points error', 'symmetry error',
       'fractal dimension error', 'worst radius', 'worst texture',
       'worst perimeter', 'worst area', 'worst smoothness',
       'worst compactness', 'worst concavity', 'worst concave points',
       'worst symmetry', 'worst fractal dimension'], dtype='<U23')

PYTHON

from pandas import DataFrame

df = DataFrame(X)

df.boxplot();

Data are differently distributed. Features with indices 3 and 23 have largest medians and variances.

Q2 Train-test split and classification of original data

Only a small training set is used.

PYTHON

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.9, random_state=RANDOM_STATE, shuffle=True)

print(X_train.shape, X_test.shape)

PYTHON

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    # Training the model using training data:
    clf.fit(X_train, y_train)

    y_predicted = clf.predict(X_test)

    # Evaluating the score using test data:
    score = clf.score(X_test, y_test)
    recall = recall_score(y_test, y_predicted)

    # Scattering two features of test data only:
    ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, s=4, cmap='bwr', marker='.')

    label = '{} - Recall Score: {:.2f}'.format(name, recall)
    ax.set_title(label , fontsize=10);

show()

Q3 Confusion Matrix

PYTHON

def plot_confusion_matrix(y_test, y_pred, classes, normalize=False, ax=None):
    """
    This function prints and plots the confusion matrix.
    y_test (array)
    y_pred (array)
    classes (array)
    normalize (bool) Normalize the results (True), or show them as integer numbers (False).
    ax Visualization axis.
    The function is an adaptation of a SciKit Learn example.
    """

    from itertools import product
    from numpy import asarray, newaxis

    from sklearn.metrics import confusion_matrix
    cm = confusion_matrix(y_test, y_pred)
    n_classes = len(classes)

    if normalize:
        cm = asarray(cm).astype('float32') / cm.sum(axis=1)[:, newaxis]

    if not ax:
        from matplotlib.pyplot import subplots
        fig, ax = subplots()

    ticks = range(n_classes)
    ax.imshow(cm, interpolation='nearest', cmap='Blues')
    ax.set_xticks(ticks)
    ax.set_xticklabels(classes, rotation=90)
    ax.set_yticks(ticks)
    ax.set_yticklabels(classes)
    fmt = '.2f' if normalize else 'd'
    thresh = 3*cm.max() / 4
    cm_dim = cm.shape

    # Matrix indices:
    indices_a = range(cm_dim[0])
    indices_b = range(cm_dim[1])
    # Cartesian product of matrix indices:
    indices = product(indices_a, indices_b)
    fmt = '.2f' if normalize else 'd'

    for ind_a, ind_b in indices:
        label = format(cm[ind_a, ind_b], fmt)
        color = "white" if cm[ind_a, ind_b] > thresh else "black"
        ax.text(ind_b, ind_a, label, ha="center", color=color)
    ax.set_ylabel('True label')
    ax.set_xlabel('Predicted label')

    return ax

PYTHON

class_names = ('False (0)', 'True (1)')

fig, axes = subplots(figsize=(17, 12), ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    clf.fit(X_train, y_train)

    y_pred = clf.predict(X_test)

    plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True, ax=ax)

    ax.set_title(name, fontsize=10);

show()

Q4 Permutation Test Score

PYTHON

n_classes = 2
chance = 1 / n_classes

fig, axes = subplots(figsize=[16, 12], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    score, permutation_scores, pvalue = permutation_test_score(clf, X, y,
                                                               scoring="accuracy",
                                                               n_jobs=1,
                                                               n_permutations=100)

    score_label = 'Score: {:.3f}, (p={:.4f})'.format(score, pvalue)

    chance_label = 'Chance: {:.3f}'.format(chance)

    ax.hist(permutation_scores)
    ax.set_ylim(0, 30)
    ax.axvline(score,  c='g', label=score_label,  linewidth=3.0)
    ax.axvline(chance, c='r', label=chance_label, linewidth=3.0)
    ax.set_title(name, fontsize=10)
    ax.legend(fontsize=8)

show()

The classification result is good in that the green score for the data is separate from the score distribution of permutated data. However, the permutated data are distributed systematically above 0.5. This is presumably due to the strongly skewed distributions of some of the features (see the boxplots above). For both SVCs, there are cases where the classifier fails to converge, and thus data are missing. (There would have been many warnings, but warnings were switched off (see abvove under ‘Import Functions’).

Q5 Normalisation

The code for three common scalers is shown below. Figures were obtained with the Normaliser. Note that this changes the y-scale of the data, but does not affect the skewness of the distribution.

PYTHON

from sklearn.preprocessing import Normalizer

norm_skl       = Normalizer()
X_normed = norm_skl.fit_transform(X)

X_normed.shape

from pandas import DataFrame

df = DataFrame(X_normed)

df.boxplot();

Train-test split and classification of normalised data

PYTHON

X_normed_train, X_normed_test, y_train, y_test = train_test_split(X_normed, y, test_size=.9, random_state=RANDOM_STATE, shuffle=True)

print(X_normed_train.shape, X_normed_test.shape)

PYTHON

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    # Training the model using trainiang data:
    clf.fit(X_normed_train, y_train)

    y_predicted = clf.predict(X_normed_test)

    # Evaluating the score using test data:
    score = clf.score(X_normed_test, y_test)
    recall = recall_score(y_test, y_predicted)

    # Scattering two features of test data only:
    ax.scatter(X_normed_test[:, 0], X_normed_test[:, 1], c=y_test, s=4, cmap='bwr', marker='.')

    label = '{} - Recall Score: {:.2f}'.format(name, recall)
    ax.set_title(label , fontsize=10);

show()

In the normalised data, the recall score is high. The SVCs even achieve scores of 1.0. The Recall is the ability of the classifier to find all the positive samples.

Confusion Matrix

PYTHON

class_names = ('False (0)', 'True (1)')

fig, axes = subplots(figsize=(17, 12), ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    clf.fit(X_normed_train, y_train)

    y_pred = clf.predict(X_normed_test)

    plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True, ax=ax)

    ax.set_title(name, fontsize=10);

show()

Notice how both SVC perform badly! All true positive were found (see above) but they struggled to detect the false negatives. In this specific case, the single recall score would be quite misleading.

If instead of the Normaliser, we apply the Standard Scaler, yielding mean 0 and variance 1 for all features, the results look a bit better.

PYTHON

from sklearn.preprocessing import StandardScaler

std_skl       = StandardScaler()
X_normed = std_skl.fit_transform(X)

df = DataFrame(X_normed)

df.boxplot();


X_normed.shape

PYTHON

X_normed_train, X_normed_test, y_train, y_test = train_test_split(X_normed, y, test_size=.9, random_state=RANDOM_STATE, shuffle=True)

print(X_normed_train.shape, X_normed_test.shape)

fig, all_axes = subplots(figsize=[15, 5], ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(all_axes.ravel(), classifiers.items()):
    # Training the model using trainiang data:
    clf.fit(X_normed_train, y_train)

    y_predicted = clf.predict(X_normed_test)

    # Evaluating the score using test data:
    score = clf.score(X_normed_test, y_test)
    recall = recall_score(y_test, y_predicted)

    # Scattering two features of test data only:
    ax.scatter(X_normed_test[:, 0], X_normed_test[:, 1], c=y_test, s=4, cmap='bwr', marker='.')

    label = '{} - Recall Score: {:.2f}'.format(name, recall)
    ax.set_title(label , fontsize=10);

show()

PYTHON

class_names = ('False (0)', 'True (1)')

fig, axes = subplots(figsize=(17, 12), ncols=4, nrows=2, sharey=True, sharex=True)

for ax, (name, clf) in zip(axes.ravel(), classifiers.items()):

    clf.fit(X_normed_train, y_train)

    y_pred = clf.predict(X_normed_test)

    plot_confusion_matrix(y_test, y_pred, classes=class_names, normalize=True, ax=ax)

    ax.set_title(name, fontsize=10);

show()

Q6 Hyperparameter Tuning

PYTHON

clf = RandomForestClassifier(random_state=RANDOM_STATE)

clf.fit(X_train, y_train)

score = clf.score(X_test, y_test)

print('Score: {:.2f}'.format(score))

PYTHON

param_grid = dict(
    n_estimators=[30, 50, 70, 90],
    max_features=[None, 'auto', 'sqrt', 'log2'],
    min_samples_split=[2, 3, 4],
    max_depth=[2, 3, 4, 5, 6]
)

cv = StratifiedShuffleSplit(test_size=0.9, random_state=RANDOM_STATE)

clf = RandomForestClassifier(random_state=RANDOM_STATE)

grid = GridSearchCV(clf, param_grid=param_grid, cv=cv, n_jobs=1)

grid.fit(X, y)

print("ORIGINAL data: Best parameters {}   Score: {:.2f}".format(grid.best_params_, grid.best_score_))

grid.fit(X_normed, y)

print("NORMED data:   Best parameters {}    Score {:.2f}".format(grid.best_params_, grid.best_score_))

PYTHON

clf = RandomForestClassifier(max_depth=4,
                             max_features=None,
                             min_samples_split=2,
                             n_estimators=50,
                             random_state=RANDOM_STATE)

clf.fit(X_train, y_train)

score = clf.score(X_test, y_test)

print('Random Forest Score: {:.2f}'.format(score))

Arbitrary parameter searches do not necessarily lead to improved performance. The reason our score differs from the score reported in the grid search is that the grid search used 10 splits into different train and test data.

Feature Importances

PYTHON

importances = clf.feature_importances_

bins = arange(importances.shape[0])

fig, ax = subplots()

ax.bar(bins, importances);
ax.set_ylabel('Feature Importance', fontsize=16);

show()

PYTHON

# Most important features
threshold = 0.1

feature_indices = bins[importances > threshold]

feature_names = data.feature_names[feature_indices]

print('Indices of features with importance above ', threshold, ':', sep='')
print(list(feature_indices))
print('Feature Name(s):', feature_names)

It turns out that with the used settings, the classification is dominated by a single feature.

Key Points

• The function permutation_test_score evaluates the significance of a cross-validated score with permutations.
• Confusion matrix demonstrates the number of correctly predicted labels against the incorrect ones.
• Adjustment of hyper-parameters of the algorithms may improve the results.
• GridSearchCV is a tool to simultaneously define different values of different parameters for optimisation.
• Progressive adjustments may lead to model over-fitting and require a validation data set.